Уравнение Шредингера для атома водорода

Исходя из представления о наличии у электрона волновых свойств, Шредингер в 1925 г. предположил, что состояние движущегося в атоме электрона должно описываться стоячей электромагнитной волны. Подставив в это уравнение вместо длины волны её значение из уравнения де-Бройля (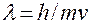), он получил новое уравнение, связывающее энергию электрона с пространственными координатами и волновой функцией, соответствующей в этом уравнении амплитуде трёхмерного волнового процесса:

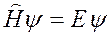
Распишем подробнее гамильтниан в уравнении Шредингера для атома водорода. Так как система состоит только из двух частиц (ядро и электрон), то связав систему отсчета с ядром, будем считать его неподвижным, а оператор кинетической энергии электрона будет иметь вид:

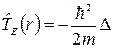, где 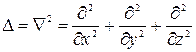- оператор Лапласа

Оператор потенциальной энергии взаимодействия електрона с ядром:

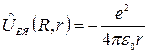
Тогда уравнении Шредингера для атома водорода можно записать:

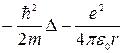() ψ = Е∙ψ (4)

Особенное значение для характеристики состояния электрона имеет волновая функция ψ. Чем больше значение 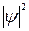в данной области пространства, тем выше вероятность того, что электрон проявит здесь свое действие, т.е. что его существование будет обнаружено в каком-либо физическом процессе.

Более точным будет следующее утверждение: вероятность обнаружения электрона в некотором малом объеме dτ выражается произведением 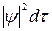. Таким образом, самая величина 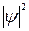выражает плотность вероятности нахождения электрона в соответствующей области пространства.

Рис.1. Электронное облако атома водорода

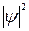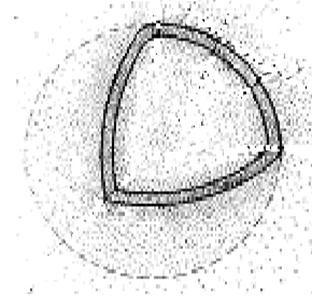
Для уяснения физического смысла квадрата волновой функции рассмотрим рис.1, на котором изображен некоторый объем вблизи ядра атома водорода. Плотность размещения точек на рис. 1 пропорциональна значению в соответствующем месте: чем больше величина 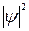, тем гуще расположены точки. Если бы электрон обладал свойствами материальной точки, то рис. 1 можно было бы получить, многократно наблюдая атом водорода и каждый раз отмечая местонахождение электрона. Плотность размещения точек на рисунке была бы тем больше, чем чаще обнаруживается электрон в соответствующей области пространства или, иначе говоря, чем больше вероятность обнаружения его в этой области. Однако, представление об электроне как в материальной точке не соответствует его истинной физической природе. Поэтому рис. 1 правильнее рассматривать как схематическое изображение электрона, "размазанного" по всему объему атома. Чтобы подчеркнуть вероятностный «размазанный» характер распределения электронов около ядра, в квантовой механике используется термин «электронное облако» в отличие от классического понятия орбита вращения электрона. Чем плотнее расположены точки в том или ином месте, тем больше здесь плотность электронного облака. Иначе говоря, плотность электронного облака пропорциональна квадрату волновой функции.

Представление в состоянии электрона как о некотором облаке электрического заряда оказывается очень удобным, хорошо передает основные особенности поведения электрона в атомах и молекулах. При этом, однако, следует иметь в виду, что электронное облако не имеет определенных, резко очерченных границ: даже на большом расстоянии от ядра существует некоторая, хотя и очень малая вероятность обнаружения электрона. Поэтому под электронным облаком условно будем понимать область пространства вблизи ядра атома, в которой сосредоточена преобладающая часть заряда и массы электрона.

В атоме водорода энергия электрона полностью определяется значением главного квантового числа n. Однако в многоэлектронных атомах энергия электрона зависит и от значения орбитального квантового числа l. Поэтому состояния электрона, характеризующиеся различными значениями l, принято называть энергетическими подуровнями электрона в атоме. Этим подуровням присвоены следующие буквенные обозначения:

Орбитальное квантовое число 0 1 2 3

Обозначение энергетического подуровня s p d f

В соответствии с этими обозначениями говорят об s-подуровне, р-подуровне и т.д. Электроны, характеризующиеся значениями орбитального квантового числа 0, 1, 2 и 3, называют, соответственно, s-электронами, p-электронами, d -электронами и f-электронами. При данном значении главного квантового числа n наименьшей энергией обладают s-электроны, затем р-, d- и f-электроны.

Рис.2. К понятию о размерах и форме электронного облака

Электронное облако не имеет резко очерченных в пространстве границ. Поэтому понятие в его размерах и форме требует уточнения. Рассмотрим в качестве примера электронное облако ls-электрона в атоме водорода (рис. 2).

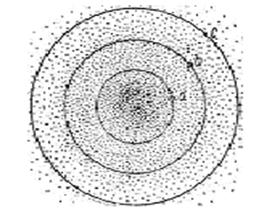
В точке а, находящейся на некотором расстоянии от ядра, плотность электронного облака определяется квадратом волновой функции 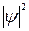. Проведем через точку a поверхность равной электронной плотности, соединяющую точки, в которых плотность электронного облака характеризуется тем же значением 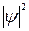. В случае ls-электрона такая поверхность окажется сферой, внутри которой заключена некоторая часть электронного облака (на рис. 2 сечение этой сферы плоскостью рисунка изображено окружностью, проходящей через точку а). Выберем теперь точку b, находящуюся на большем расстоянии от ядра, и также проведем через нее поверхность равной электронной плотности. Эта поверхность тоже будет обладать сферической формой, но внутри ее будет заключена большая часть электронного облака, чем внутри сферы радиусом а. Пусть, наконец, внутри поверхности равной электронной плотности, проведенной через некоторую точку с, заключена преобладающая часть электронного облака; обычно эту поверхность проводят так, чтобы она заключала 90% заряда и массы электрона. Такая поверхность называется граничной поверхностью, и именно её форму и размеры принято считать формой и размерами электронного облака. Граничная поверхность ls-электрона представляет собой сферу, однако граничные поверхности р- и d-электронов имеют более сложную форму.

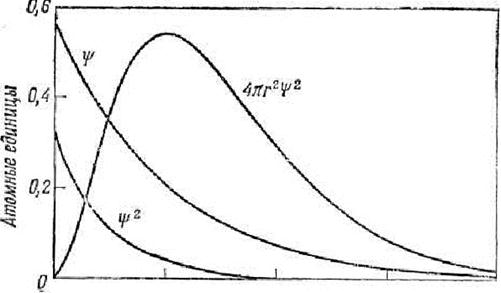
На рис.3 изображены значения волновой функции ψ и её квадрата для ls-электрона в зависимости вот расстояния от ядра r.

r, ат.ед.

Рис.3. Волновые функции и плотности вероятности для состояния с наименьшей энергией (1s) атома водорода.

Рис. 3 показывает также, что при увеличении расстояния от ядра величина 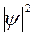монотонно убывает. Это означает, что по мере удаления от ядра плотность электронного облака ls-электрона уменьшается. Это не означает, однако, что с ростом r вероятность обнаружить ls-электрон тоже монотонно убывает. Как уже указывалось, вероятность обнаружения электрона в некотором малом объеме dτ выражается произведением 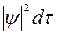. В случае ls-электрона (см.рис.2) 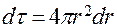; следовательно, вероятность обнаружения электрона в сферическом слое, заключённом между сферами с радиусам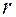и и 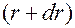, пропорциональна величине 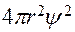. Зависимость величины 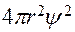от 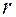для ls-электрона изображена на рис.3 (подобные графики называют графиками радиального распределения вероятности нахождения электрона). Как показывает рис.3,вероятность обнаружить ls-электрон на малых расстояниях от ядра близка к нулю, т.к. 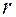мало. Ничтожно мала вероятность обнаружения электрона на очень большом расстоянии от ядра: здесь близок к нулю множитель 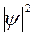. На некотором расстоянии от ядра 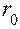вероятность обнаружения электрона имеет максимальное значение. Для атома водорода это расстояние равно 0.53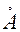, что совпадает с вычисленным Бором значением радиуса ближайшей к ядру орбиты электрона. Однако трактовка этой величины в теории Бора и с точки зрения квантовой механики различна. Согласно Бору, электрон в атоме водорода находится на расстоянии 0.53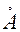от ядра, а с позиции квантовой механики этому расстоянию соответствует лишь максимальная вероятность обнаружения электрона. Электронные облака р-, d- электронов имеет более сложную форму (см.рис.4).

Итак, боровское понятие «орбита электрона» в квантово-механической модели заменилось представлением об «электронном облаке». Позднее оно было конкретизировано и заменено понятием об атомной орбитали, отвечающей определённой совокупности вероятных положений электрона в атоме, которая описывается функцией 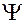; в первом приближении можно сказать, что квантовые числа n, l, m определяют геометрию атомной орбитали.

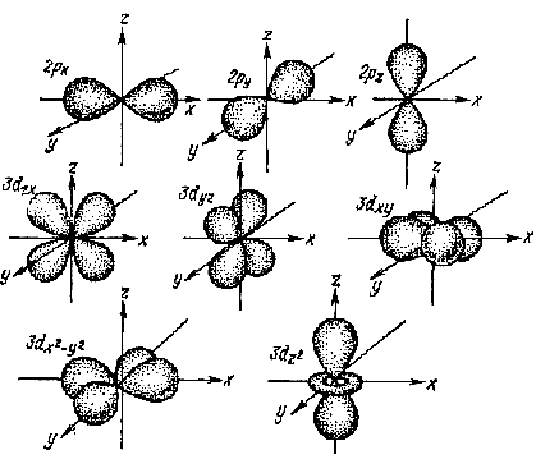
Рис. 4. Формы и пространственная ориентация электронных облаков 2р- и Зd-электронов.

Дата добавления: 2014-01-20