
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ точности определения оценок коэффициентов регрессии. Так как выборочные данные являются случайными величинами, оценки и также являются случайными величинами
|
|
|
|
Так как выборочные данные являются случайными величинами, оценки 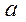 и
и 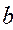 также являются случайными величинами. В случае выполнения условий Гаусса-Маркова, оценки будут несмещенными и состоятельными. При этом они будут тем надежнее, чем меньше их разброс вокруг их математических ожиданий или меньше их дисперсия. Надежность получаемых оценок тесно связана с D(
также являются случайными величинами. В случае выполнения условий Гаусса-Маркова, оценки будут несмещенными и состоятельными. При этом они будут тем надежнее, чем меньше их разброс вокруг их математических ожиданий или меньше их дисперсия. Надежность получаемых оценок тесно связана с D(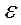 ). Как уже известно
). Как уже известно  ,
, 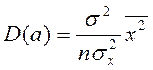 . Из соотношений можно сделать следующие очевидные выводы:
. Из соотношений можно сделать следующие очевидные выводы:
1) дисперсии 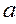 и
и 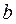 прямо пропорциональны D(
прямо пропорциональны D(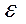 ) =
) = 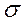 2;
2;
2) чем больше число наблюдений, тем меньше дисперсия;
3) чем больше 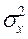 (разброс х), тем меньше дисперсии оценок.
(разброс х), тем меньше дисперсии оценок.
Так как случайные составляющие по выборке определены быть не могут, при анализе надёжности оценок коэффициентов регрессии они заменяются наблюдаемыми отклонениями 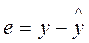 , а дисперсии случайных отклонений D(
, а дисперсии случайных отклонений D(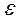 ) =
) = 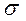 2 заменяются несмещенной оценкой
2 заменяются несмещенной оценкой 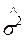 =
= 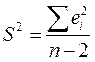 (здесь (n-2) – число степеней свободы). S – называют стандартной ошибкой регрессии. Тогда оценки дисперсий оценок
(здесь (n-2) – число степеней свободы). S – называют стандартной ошибкой регрессии. Тогда оценки дисперсий оценок
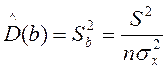 и
и 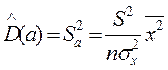 ,
,
S a и Sb – стандартные ошибки коэффициентов регрессии.
Пример. Получим оценки S2, S a, Sb для условий примера из лекции 2.
| № предприятия | |||||||
| Выпуск продукции, х | |||||||
| Затраты на производство, у |
Решение
Ранее было получено уравнение регрессии
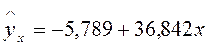 , с использованием которого можно было рассчитать модельные значения
, с использованием которого можно было рассчитать модельные значения 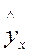 . Чтобы получить стандартные ошибки, необходимо:
. Чтобы получить стандартные ошибки, необходимо:
1)  n = 7;
n = 7;
S2 = 263,1583/5 = 52,632; S = 7,255;
2) 
3) Sb2 = 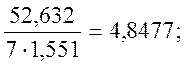 Sb = 2,202;
Sb = 2,202;
4) S a 2 = 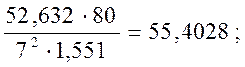 S a = 7,443.
S a = 7,443.
Стандартные ошибки регрессии и её коэффициентов можно получить при использовании ППП Excel (см. Вывод итогов).
Если выполняется условие нормальности распределения случайного члена: 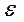 ~ N(0;
~ N(0;  ), то МНК оценки коэффициентов регрессии тоже нормальны с соответствующими параметрами, так как они являются линейными функциями от Уt:
), то МНК оценки коэффициентов регрессии тоже нормальны с соответствующими параметрами, так как они являются линейными функциями от Уt:
 ~ N(
~ N(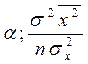 ) и
) и 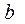 ~ N(
~ N( ).
).
Если условие нормальности ошибок не выполняется, то при некоторых условиях регулярности и росте n можно считать это распределение асимптотически нормальным.
Во время статистических исследований всегда проверяют гипотезы:
Н0: а = а 0 или «о значимости» Н0: а = 0
Н0: b = b0 Н0: b = 0.
Альтернативная гипотеза (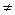 ) предусматривает построение двусторонней критической области. В качестве критерия проверки используют случайные величины, называемые
) предусматривает построение двусторонней критической области. В качестве критерия проверки используют случайные величины, называемые
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,991189256 | |||||
| R-квадрат | 0,98245614 | |||||
| Нормированный R-квадрат | 0,978947368 | |||||
| Стандартная ошибка | 7,254762501 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 14736,84211 | 14736,84211 | 1,39294E-05 | |||
| Остаток | 263,1578947 | 52,63157895 | ||||
| Итого | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -5,789473684 | 7,443229276 | -0,777817459 | 0,47185877 | -24,92290365 | 13,34395628 |
| x | 36,84210526 | 2,201736912 | 16,73320053 | 1,39294E-05 | 31,18236035 | 42,50185017 |
t-статистиками: tb = 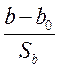 или ta =
или ta = 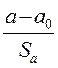 ; которые имеют распределение Стьюдента с (n-2) степенями свободы. Проверка состоит в следующем:
; которые имеют распределение Стьюдента с (n-2) степенями свободы. Проверка состоит в следующем:
- если 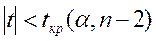 , то нет оснований отвергать Н0;
, то нет оснований отвергать Н0;
- если  , то Н0 отвергают.
, то Н0 отвергают.
При оценке значимости коэффициентов линейной регрессии на начальном этапе можно использовать «грубое» правило:
1) если стандартная ошибка коэффициента больше его по модулю ( ), то коэффициент не значим (надежность меньше 0,7);
), то коэффициент не значим (надежность меньше 0,7);
2) если  , то оценка может рассматриваться как относительно значимая, 0,7 <
, то оценка может рассматриваться как относительно значимая, 0,7 <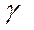 <0,95;
<0,95;
3) 2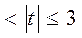 , то оценка значима, 0,95 <
, то оценка значима, 0,95 <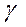 <0,99;
<0,99;
4) 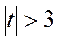 , это почти гарантия наличия линейной связи.
, это почти гарантия наличия линейной связи.
В каждом конкретном случае имеет значение число наблюдений. Чем их больше, тем надежнее при прочих равных условиях выводы о значимости коэффициентов. При n>10 «грубое» правило практически всегда работает.
Соответствующие доверительные интервалы для оценок коэффициентов регрессии с надёжностью 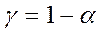 имеют вид: (
имеют вид: (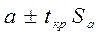 ) и (
) и (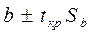 ).
).
Пример. Проверим гипотезу Н0: b = 37 при  и 0,05 для нашего примера.
и 0,05 для нашего примера.
1) 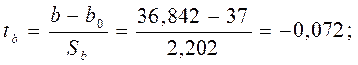
2) tкр.дв(0,01;5) = 4,03; tкр.дв(0,05;5) = 2,57;
3) Так как 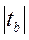 = 0,072 < tкр.дв(0,05;5) = 2,57, то нет оснований отвергать Н0.
= 0,072 < tкр.дв(0,05;5) = 2,57, то нет оснований отвергать Н0.
Если Н0 отвергается при  , то она будет отвергнута и при
, то она будет отвергнута и при 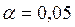 . Если Н0 не отвергается при
. Если Н0 не отвергается при 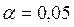 , то она не будет отклоняться и при
, то она не будет отклоняться и при 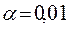 автоматически. Стандартные ППП содержат проверку «значимости» полученных оценок. При этом если Н0: b = 0 не отклоняется, то коэффициент b статистически не значим, то есть нет зависимости между Х и У.
автоматически. Стандартные ППП содержат проверку «значимости» полученных оценок. При этом если Н0: b = 0 не отклоняется, то коэффициент b статистически не значим, то есть нет зависимости между Х и У.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 673; Нарушение авторских прав?; Мы поможем в написании вашей работы!