Структуры полей в прямоугольных волноводах и методика их построения

Лекция №20

Рассмотрим структуры полей в прямоугольном волноводе для Н -волн (, ). Напряженности поперечных компонент полей выражаются через продольные магнитные компоненты формулами (18а),

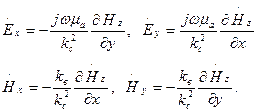
После подстановки в эти формулы выражения для продольных компонент, (19.36),

, ,

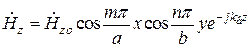где 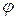- начальная фаза, были получены с точностью до множителя следующие значения поперечных компонент полей 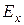, , , 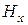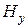(формулы (19.32), (19.33), (19.34), (19.35)),

,

,

,

,

,

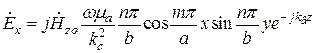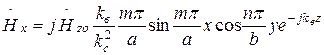Запишем выражения для этих полей в вещественной форме. При этом учитываем, что умножение на 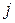и на – j эквивалентно сдвигу фазы колебания на и -соответственно. Действительно

,

.

Домножив выражения (19.32–19.36) на ранее сокращённый множитель и выделив из этих выражений их действительные части, находим:

,

,

,

,

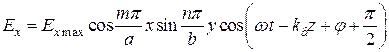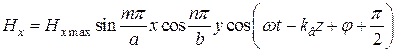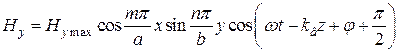, (20.1)

,

, ,

, .

Видно, что поперечные составляющие находятся в фазе или в противофазе, а продольная составляющая 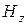по отношению к поперечным сдвинута на . Функции при вещественном свидетельствуют о наличии бегущих волн. По осям x и y существуют стоячие волны.

Поперечные компоненты поля 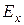, , , 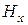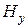дадут значения вектора Умова-Пойтинга 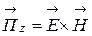направленного вдоль волновода, т.е. вдоль оси z.

Эти компоненты находятся в фазе или в противофазе и при перемножении будут всегда иметь направления распространения вдоль оси волновода..

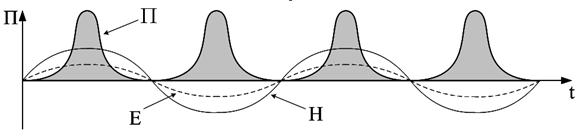
Рис. 20.1. Вектор Умова-Пойтинга для поперечных компонент Е и Н

Поперечные значения полей и с продольной сдвинуты по фазе на . Вектор Умова-Пойтинга, образованный этими компонентами будет знакопеременным, что свидетельствует о колебании энергии поля по направлению при распространении от одной стенки волновода к другой.

Рис. 20.2. Вектор Умова-Пойтинга для поперечных компонент 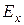, и
продольной 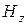компонент поля

Наличие продольной компоненты вектора Умова-Пойтинга и колеблющейся компоненты между стенками волновода даёт основание считать, что энергия переносится вдоль волновода последовательно отражаясь от его стенок, рис.20.3.

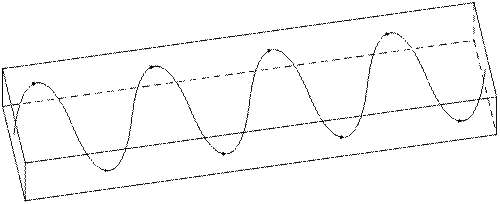
Рис. 20.3. Распространение энергии поля в волноводе

В волноводе может существовать множество полей с различными значениями индексов.

Рассмотрим простейшую и наиболее часто используемую волну () с индексами m =1, n =0. В этом случае

, ,

, ,

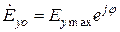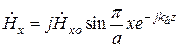, , (20.2)

, .

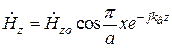С учетом множителя вещественные значения полей соответственно примут вид:

,

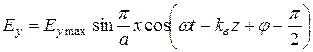, (20.3)

,

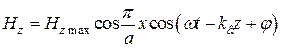или

,

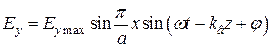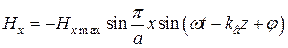. (20.4)

Построение структуры (картины) распределения полей целесообразно начинать с построения изображения распределения силовых линий электрического поля. Поля целесообразно рассматривать в сечениях t =const, x =const, y =const, z =const. Значение начальной фазы 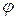примем равным нулю, т.е. .

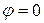При t =0, 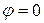и , ,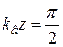

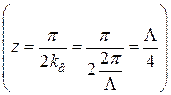картина силовых линий полей

,

,

,

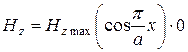показана на рис. 20.4.

Непосредственно при поле , но в точках, близких к поле .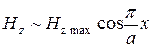

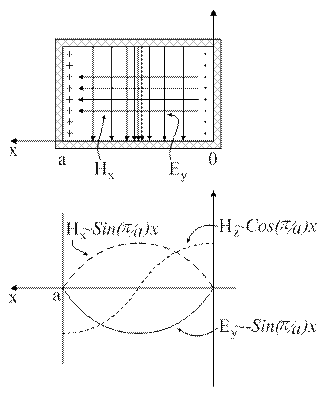
Рис. 20.4. Картина силовых линий полей

Рассмотрим теперь сечение при рис.20.5.

При этом

,

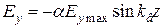, (20.5)

.

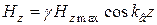Рис.20.5. Поля в сечении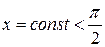

На рис.20.5 ось x направлена перпендикулярно странице от читателя.

Крестиками обозначены силовые линии поля. 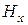направленные от читателя, точками – к читателю. Силовые лини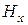и и 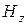совместно замкнуты. Поля 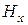и противофазны (сдвинуты на друг относительно друга). По отношению к полю 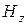они сдвинуты на .

Рассмотрим теперь сечение y =const. От y эти поля не зависят, т.е. одинаковы в любом сечении, рис. 20.6

Рис. 20.6. Поля в сечении y =const

Здесь крестиками и точками обозначены следы электрического поля .

Критическая частота, для волны

. (20.6)

Критическая длина волны

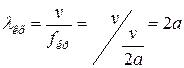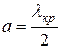,. (20.7)

Эта длина волны не зависит от величины размера «b».

Рекомендации по выбору размеров поперечного сечения волновода следующие:

1. Размер «а» необходимо выбирать из условия 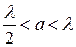. Обычно 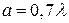. В противном случае может возникнуть волна .

2. Размер «b» необходимо выбирать из условия . Иначе может возникнуть волна . Минимальный размер «b» ограничивается напряжением пробоя и рассчитывается по формуле

, (20.8)

где Р [кВт] – средняя мощность волны в волноводе, 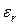- относительная диэлектрическая проницаемость, 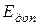- допустимое пробивное напряжение среды, заполняющей волновод.

Дата добавления: 2014-01-20