Детерминированные модели

I. Простейшая модель M1 оптимального размера заказа.

Предпосылки:

1) Темп спроса на товар известен и постоянен.

2) Получение заказа мгновенно.

3) Закупочная цена не зависит от размера заказа.

4) Не допускается дефицит.

Исходные данные: темп спроса, издержки заказа и хранения.

Результат: оптимальный размер заказа, время между заказами, количество заказов за фиксированный период времени, совокупные издержки.

Размер заказа является постоянным. Заказ выполняется мгновенно. Уровень запасов убывает с постоянной интенсивностью, пока не достигает нулевого значения. В этот момент времени делается, мгновенно выполняется и поступает заказ, размер которого равен Q и уровень запаса восстанавливается до максимального значения. При этом оптимальным решением задачи будет тот размер заказа Q*, при котором минимизируются общие издержки за период, равные сумме издержек хранения и издержек заказа.

Динамика изменения количества продукта на складе показана на следующем рисунке:

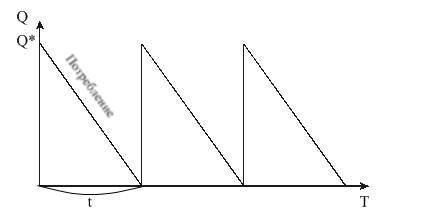
Рис. 1

Пусть:

Q — размер заказа;

T — протяженность периода планирования;

D — величина спроса за период планирования;

d — величина спроса в единицу времени;

K — издержки заказа (затраты на транспортировку, доставку продукции);

H — удельные издержки хранения за период;

h — удельные издержки хранения в единицу времени;

Тогда:

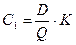— издержки заказа;

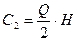— издержки хранения;

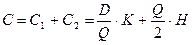— совокупные издержки.

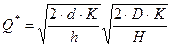— оптимальный размер заказа (определяется по формуле Вильсона).

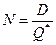— оптимальное число заказов за период;

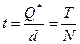— время цикла (оптимальное время между заказами).

Вывод формулы оптимального заказа:

;

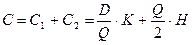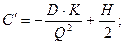
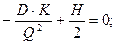
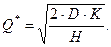
II. Модель M2 оптимального размера заказа с фиксированным временем его выполнения.

Предпосылки:

1) Темп спроса на товар известен и постоянен.

2) Время выполнения заказа известно и постоянно.

3) Закупочная цена не зависит от размера заказа.

4) Не допускается дефицит.

Исходные данные: темп спроса, издержки заказа и хранения, время выполнения заказа.

Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса, количество заказов за фиксированный период времени, совокупные издержки.

Размер заказа является постоянным. Время выполнения заказа постоянно. Уровень запасов убывает с постоянной интенсивностью, пока не достигает точки восстановления R.

Точка восстановления — запас продукта, при котором нужно сделать очередной заказ. В этот момент времени делается заказ, который выполняется за время L. К моменту поступления заказа размер запаса на складе равен нулю. Оптимальным решением задачи будет тот размер заказа Q*, при котором минимизируются общие издержки за период, равные сумме издержек хранения и издержек заказа.

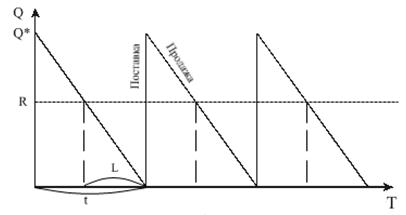
Рис. 2

Пусть:

Q — размер заказа;

T — протяженность периода планирования;

D — величина спроса за период планирования;

d — величина спроса в единицу времени;

K — издержки заказа (затраты на транспортировку, доставку продукции);

H — удельные издержки хранения за период;

h — удельные издержки хранения в единицу времени;

L — количество дней поставки (период поставки товарной продукции).

Тогда:

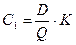— издержки заказа;

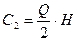— издержки хранения;

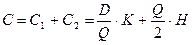— совокупные издержки.

Кривые издержек заказа, издержек хранения и совокупных издержек указаны на следующем рис. 2:

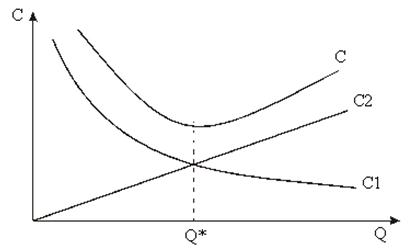
Рис. 3

Экстремум функции — минимум совокупных (полных) затрат определяют оптимальный размер заказа.

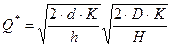— оптимальный размер заказа (определяется по формуле Вильсона).

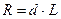— точка заказа — это то количество товарной продукции, которое остается на складе, когда делается заявка на поставку следующей партии.

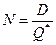— оптимальное число заказов за период;

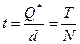— время цикла (оптимальное время между заказами).

Следует обратить внимание на то, что оптимальный размер заказа не зависит от цены продукта.

III. Модель M3 с производством.

Предпосылки:

1) Темп спроса на товар известен и постоянен.

2) Темп производства товара известен и постоянен.

3) Время выполнения заказа известно и постоянно.

4) Закупочная цена не зависит от размера заказа.

5) Не допускается дефицит.

Исходные данные: темп спроса, темп производства, издержки заказа, издержки хранения, время выполнения заказа.

Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса.

Фирма производит продукт самостоятельно, хранит его на складе и расходует с постоянным темпом. Если темп производства выше темпа спроса, то излишки продукта накапливаются на складе. Когда количество продукта на складе достигает максимального значения, производство прекращается и продукт расходуется со склада с постоянным темпом. Когда запас на складе достигает точки восстановления, производство возобновляется. При этом оптимальным решением задачи будет тот размер заказа Q*, при котором минимизируются общие издержки за период, равные сумме издержек хранения и издержек на возобновление производства.

Динамика изменения количества продукта на складе показана на следующем рис.3

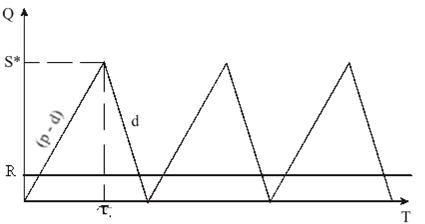
Рис. 4

Пусть:

Q — размер заказа;

p — темп производства;

T — протяженность периода планирования;

D — величина спроса за период планирования;

d — величина спроса в единицу времени;

K — фиксированные издержки на запуск производства.

H — удельные издержки хранения за период;

h — удельные издержки хранения в единицу времени;

L — время, необходимое для запуска производства;

τ — определенный момент времени;

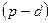— темп накопления продукции;

Тогда:

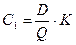— издержки заказа;

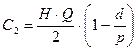— издержки хранения;

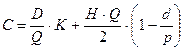— совокупные издержки;

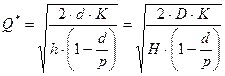— оптимальный размер заказа;

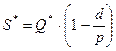— максимальный уровень запасов;

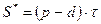— накопление продукции на момент τ;

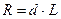— точка заказа;

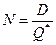— оптимальное число заказов за период;

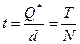— время цикла (оптимальное время между заказами).

В этой модели оптимальный размер заказа также не зависит от цены продукта.

Вывод формулы оптимального заказа:

;

;

;

.

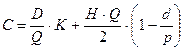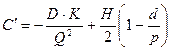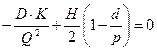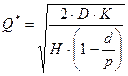IV. Модель M4 оптимального размера заказа с дефицитом.

Предпосылки:

1) Темп спроса на товар известен и постоянен.

2) Время выполнения заказа известно и постоянно.

3) Закупочная цена не зависит от размера заказа.

Исходные данные: темп спроса, издержки заказа, издержки хранения, издержки дефицита.

Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса, количество заказов за фиксированный период времени, совокупные издержки.

Размер заказа является постоянным. Уровень запасов убывает с постоянной интенсивностью. Допускается дефицит продукта. После получения заказа фирма компенсирует дефицит и восстанавливает запас продукта на складе. Заказ делается тогда, когда дефицит продукта на складе достигает оптимального размера. Оптимальным решением задачи будет такой размер заказа Q*, при котором минимизируются общие издержки за период, равные сумме издержек хранения и издержек заказа.

Динамика изменения количества продукта на складе показана на следующем рис. 4.:

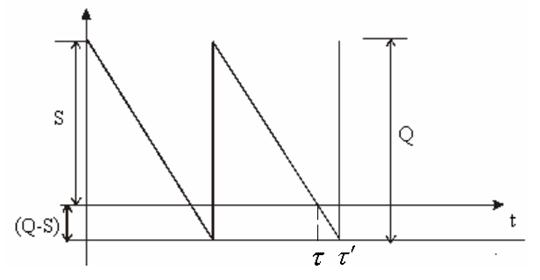
Рис. 5

Пусть:

Q — размер заказа;

T — протяженность периода планирования;

D — величина спроса за период планирования;

d — величина спроса в единицу времени;

K — издержки заказа;

H — удельные издержки хранения за период;

h — удельные издержки хранения в единицу времени;

B — упущенная прибыль за период, возникающая в результате дефицита одной единицы продукта;

S —запас за единицу времени;

b — упущенная прибыль в единицу времени, возникающая в результате дефицита одной единицы продукта;

Тогда:

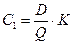— издержки заказа;

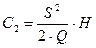— издержки хранения;

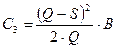— издержки дефицита;

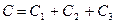— совокупные издержки;

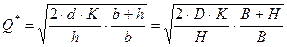— оптимальный размер заказа;

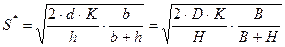— максимальный размер запаса;

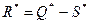— максимальный дефицит;

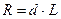— точка восстановления;

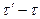— время товарного дефицита.

Вывод формулы оптимального заказа:

;

;

;

;

;

;

;

;

;

.

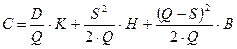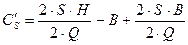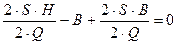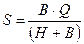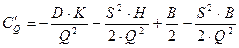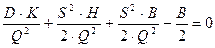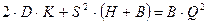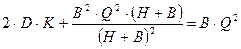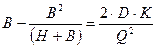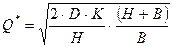V. Модель M5 с количественными скидками.

Предпосылки:

1) Темп спроса на товар известен и постоянен.

2) Время выполнения заказа известно и постоянно.

Исходные данные: темп спроса, издержки заказа, издержки хранения, цена товара, количественные скидки в случае закупки крупных партий товара.

Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса, количество заказов за фиксированный период времени, совокупные издержки.

Пусть:

Q — размер заказа;

T — протяженность периода планирования;

D — величина спроса за период планирования;

d — величина спроса в единицу времени;

K — издержки заказа;

H — удельные издержки хранения за период;

h — удельные издержки хранения в единицу времени.

Предположим, что известны числа 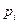, , 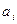, 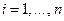где 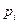— цена продукта при размере заказа Q в интервале .

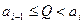Тогда:

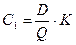— издержки заказа;

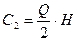— издержки хранения;

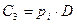— издержки на закупку товара;

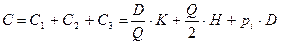— совокупные издержки.

Тогда оптимальный размер заказа определяется в результате решения n задач. Каждая из этих задач сводится к определению такого размера заказа 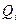, , 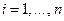при котором функция совокупных издержек достигает минимума при ограничениях 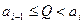. Решение исходной задачи определяется из условия .

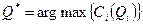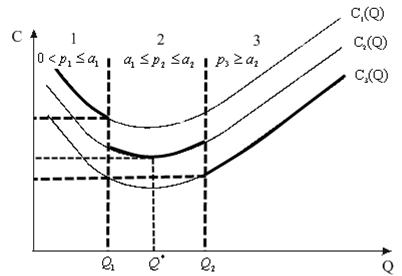
Рис. 6

Значение цены 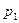определено на интервале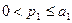, значение цены 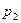определено на интервале 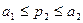, значение цены 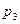определено на полуинтервале .

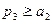Необходимо рассматривать точки на границах, где цена меняет свое значение.

Соответственно, функция общих издержек 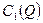определена при значении цены 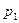на интервале 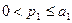, функция общих издержек 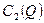определена при значении цены 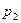на интервале 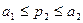, функция общих издержек 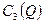определена при значении цены 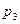на полуинтервале .

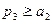Дата добавления: 2014-01-20