Определение вероятности

Рассмотрим стохастический эксперимент и случайное событие A, наблюдаемое в этом эксперименте. Повторим этот эксперимент n раз и пусть m(A) - число экспериментов, в которых событие A произошло. Относительной частотой события A в проведенной серии экспериментов назовём отношение

. (1.1)

Легко убедиться в справедливости свойств: если A и B несовместны (АВ = Æ), то .

Относительная частота определяется только после проведения серии экспериментов и, вообще говоря, может меняться от серии к серии. Однако опыт показывает, что во многих случаях при увеличении числа опытов относительная частота приближается к некоторому числу. Этот факт устойчивости относительной частоты неоднократно проверялся и может считаться экспериментально установленным. Мы уже говорили, что если бросить две тонны монет, то примерно одна тонна упадет кверху гербом, то есть относительная частота выпадения герба примерно равна 0,5.

Если при увеличении числа опытов относительная частота события n (A) стремится к некоторому фиксированному числу, то говорят, что событие A стохастически устойчиво, а это число, обозначаемое р(A), называют вероятностью события A. Это определение называют статистическим определением вероятности.

Рассмотрим некий стохастический эксперимент, и пусть пространство его элементарных событий состоит из конечного или бесконечного (но счётного) множества элементарных событий w₁, w₂,...,w_i,.... Предположим, что каждому элементарному событию w_iприписан некоторый ¢¢вес¢¢ - p _i, удовлетворяющий следующим свойствам:

p i ³ 0, . (1.2)

В этом случае p _iназовём вероятностью элементарного события w_i.

Пусть теперь A - случайное событие, наблюдаемое в этом опыте, и ему соответствует некоторое множество АÍW.

Назовём вероятностью события A сумму вероятностей элементарных событий, благоприятствующих A (входящих в соответствующее множество A):

(1.3)

Введённая таким образом вероятность обладает теми же свойствами, что и относительная частота: ; если AB = Æ, p(A + B) = p(A) + p(B).

Действительно, согласно (1.3)

,

.

В последнем соотношении мы воспользовались тем, что ни одно элементарное событие не может благоприятствовать одновременно двум несовместным событиям.

Особо отметим, что теория вероятностей не указывает способов определения p i, их надо искать из соображений практического характера или получать из соответствующего статистического эксперимента.

В качестве примера рассмотрим классическую схему теории вероятностей. Для этого рассмотрим стохастический эксперимент, пространство элементарных событий которого состоит из конечного (n) числа элементов. Предположим дополнительно, что все эти элементарные события равновозможны, то есть вероятности элементарных событий равны p (w_i) = p _i= p. Отсюда следует, что

или .

Пример. При бросании симметричной монеты выпадение герба и решки равновозможны, их вероятности равны 0,5.

Пример. При бросании симметричного кубика все грани равновозможны, их вероятности равны 1/6.

Пусть теперь событию A благоприятствует m элементарных событий, их обычно называют благоприятными исходами. Тогда

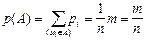Þ 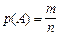. (1.4)

Таким образом, в классической схеме вероятность случайного события A равна отношению числа исходов, благоприятствующих A, к общему числу равно возможных исходов.

Пример. В урне лежит m белых шаров и n черных. Чему равна вероятность вытащить белый шар?

Решение. Всего элементарных событий m+n. Они все равновероятны. Благоприятных из них m. Следовательно, P = m/(m+n).

При подсчёте числа исходов часто используются некоторые правила и формулы комбинаторики, которые и приведём ниже.

Правило произведения. Если из некоторого множества A элемент a_i можно выбрать k _A способами, а элемент b_j из множества В - k _B способами, то совокупность (a_i, b_j) можно образовать k _A ×k _B способами. Правило верно и для совокупностей, состоящих из большего, чем 2, числа элементов.

Пример. Бросают два кубика – белый и красный. Элементарное событие - на белом выпало число a, на красном - b. Всего элементарных событий (a,b) 36 = 6×6 штук.

Дата добавления: 2014-01-20