Модели бинарного выбора

Для наглядности будем рассматривать модели бинарного выбора на примере покупки семьей автомобиля. Будем считать, что зависимая переменная у = 1, если в течение исследуемого периода времени семья купила автомобиль, и у = 0 в противном случае. Ясно, что на решение о покупке автомобиля влияют самые разные факторы: доход семьи, количество ее членов, их возраст, место проживания семьи и т.д. Набор этих характеристик можно представить вектором 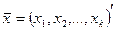(независимые переменные). Будем полагать также, что на решение семьи влияют также неучтенные случайные факторы (ошибки). Выдвигая различные предположения о характере зависимости у от х, будем получать разные модели. Мы рассмотрим три модели: линейную модель вероятности и так называемые probit- и logit- модели.

2.1. Линейная модель вероятности

Воспользуемся обычной линейной моделью регрессии:

где t – номер наблюдения (семьи),

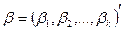– набор неизвестных параметров (коэффициентов);

ε_t – случайная ошибка.

Так как y_t принимает значения 0 или 1 и М(ε_t) = 0, то

Таким образом, модель (1) может быть записана в виде

поэтому ее называют линейной моделью вероятности.

Отметим некоторые особенности этой модели, наличие которых не позволяет успешно применять МНК для оценивания коэффициентов b и прогнозирования.

Из (1) следует, что ошибка ε в каждом наблюдении может принимать только два значения: 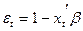с вероятностью P(y_t = 1) и 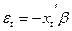с вероятностью 1 – P(y_t = 1). Это не позволяет считать ошибку нормально распределенной. Далее, непосредственным вычислением получаем, что дисперсия ошибки

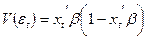
зависит от x_t, т.е. модель (1) гетероскедастична. Как известно, оценки коэффициентов b, полученные обычным МНК, в этом случае не являются эффективными, и желательно пользоваться обобщенным МНК.

Самым серьезным недостатком линейной модели вероятности является тот факт, что прогнозные значения 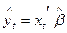, которые по смыслу модели есть прогнозные значения вероятности P(y_t = 1), могут лежать вне отрезка [0; 1], что не поддается разумной интерпретации. Это существенно ограничивает область применимости линейной модели вероятности. Ее целесообразно использовать при большом числе наблюдений и при достаточно точной спецификации модели, а также как инструмент первичной обработки данных для сравнения с результатами, получаемые более тонкими методами.

Дата добавления: 2014-01-20