Ковариационная матрица оценок коэффициентов регрессии. Оценка дисперсии ошибок

Преобразуем вектор оценок 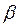с учетом наличия случайной составляющей:

,

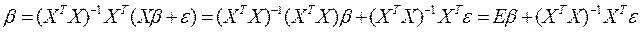Т.е. оценки параметров, найденные по выборке, будут содержать случайные ошибки.

Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной

, .

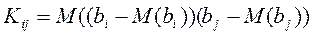Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных. Так как 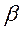является несмещенной оценкой, то

, .

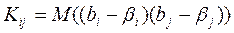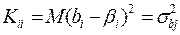В матричном виде будем иметь

,

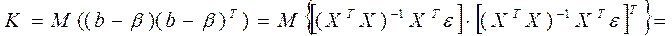
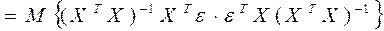
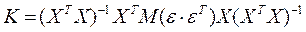так как эти элементы Х – детерминированные величины.

В матрице 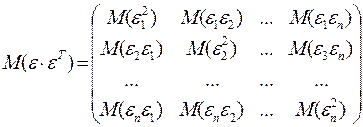все элементы, не лежащие на главной диагонали, равны нулю в силу некоррелируемости и 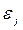между собой, а все элементы, лежащие на главной диагонали равны одной и той же дисперсии 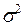: . Поэтому 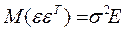и, следовательно, ковариационная матрица

.

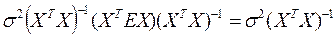Так как 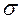² неизвестна, заменив её несмещённой оценкой – выборочной дисперсией,

,

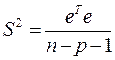где (n-p-1) – число степеней свободы, получим выборочную оценку ковариационной матрицы. Стандартные ошибки коэффициентов регрессии определяются:

1способ: 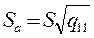, , 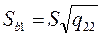…, где q_ii – диагональные элементы матрицы (Х^ТХ)^-1.

		6,613734	-0,46567	-0,31974
	XtX-1=	-0,46567	0,085837	-0,04936
		-0,31974	-0,04936	0,11588
		y^	y-y^
		5,133047	-0,13305		S^2=	0,454936
		9,317597	0,682403		S=	0,674489
		10,54077	-0,54077		Sa=	1,734596
		6,356223	0,643777
		5,476395	-0,47639		Sb1=	0,197611
		5,648069	0,351931
		6,527897	-0,5279		Sb2=	0,229604
		СУММКВ	1,819742

2 способ: , где R² – множественный коэффициент детерминации, R²_xix1…xp – коэффициент детерминации для зависимости x_i от остальных факторов.

Дата добавления: 2014-01-20