Функция распределения Ферми–Дирака

Элементы квантовой статистики. Плотность состояний.

Лекция 8

Системы, состоящие из огромного числа частиц, описываются вероятностными (статистическими) характеристиками и закономерностями. Статистические характеристики системы не присущи отдельной частице. Именно так для идеального газа формируется понятия давления и температуры. Такой подход справедлив не только для классических систем, но и для квантовых.

Квантовая статистика - раздел статистической физики, в котором исследуется системы, состоящие из огромного числа частиц, подчиняющихся законам квантовой механике.

В классической системе, даже если она представлена идеальным газом, состоящим из одинаковых молекул, частицы различимы. Они могут быть просто пронумерованы, а если это невозможно, то знание координат и импульсов в начальный момент времени всегда позволит рассчитать положение частицы в последующие моменты времени. И, если две одинаковые частицы, находящиеся в разных состояниях, поменяются местами, то состояние системы изменится.

В квантовых системах статистика существенно меняется. Прежде всего, потому, что в них действуют принцип неразличимости тождественных частиц. Если две тождественные частицы, находящиеся в разных квантовых состояниях, поменяются местами, то состояние системы не изменится.

В квантовой теории все частицы делятся на фермионы и бозоны. Бозоны - частицы с целым значением спина, фермионы - частицы с полуцелым спином. Принцип Паули запрещает двум и более фермионам находиться в системе с одинаковым набором квантовых чисел (в одинаковом состоянии). Для бозонов такие ограничения не действуют. Поэтому статистики фермионов и бозонов различаются. Фермионы описываются статистикой Ферми-Дирака, а бозоны - статистикой Бозе-Эйнштейна.

Так как в низкоразмерных квантовых структурах носителями заряда являются электроны (и дырки), которые в свою очередь являются фермионами, то ограничимся рассмотрением только статистики Ферми-Дирака.

Свободные носители заряда – электроны, каждый из которых независимо от остальных принимает в твёрдом теле то или иное состояние, в условиях теплового равновесия всё же имеют объективные меры, посредством которых описываются совокупные свойства всего ансамбля. К таким мерам относится функция распределения.

Функция распределения в статистических системах показывает относительное число членов ансамбля, обладающих данным свойством. Конкретно в случае электронов она показывает, какую долю от общего числа свободных электронов составляют электроны с заданной энергией Е. Как отмечалось максимальное число электронов, которые могут иметь данную энергию является ограниченным, значит, число разрешённых состояний в единице объёма, приходящихся на единичный интервал энергии 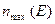[Дж^-1 см^-3 ], есть строго определённая для заданной энергии величина. Значит, функция распределения 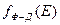определяет отношение числа электронов n(Е), реально занимающих энергетический уровень Е, к максимальному числу электронов, которые в принципе могут находиться на данном уровне:

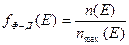(1.1)

Аналитическое выражение функции распределения электронов, которое независимо друг от друга предложили итальянский физик Энрико Ферми и английский физик Поль Дирак, имеет вид

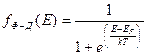(1.2)

где параметр E_F − уровень Ферми. Функция Ферми−Дирака, как элемент универсального математического аппарата, не зависит от свойств той или иной конкретной системы, а зависит лишь от температуры. Привязка к конкретной системе осуществляется через параметр E_F, который показывает, как нужно располагать функцию Ферми−Дирака относительно энергетических уровней конкретной системы.

Функция распределения позволяет решать ряд важных задач, необходимых для анализа полупроводниковых приборов.

Во-первых, представляется возможным определять распределение свободных носителей заряда по энергиям. Распределение электронов в пределах зоны проводимости получаем из (1.1):

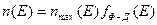[см^-3Дж^-1] (1.3а)

Если энергетический уровень заполнен не полностью, то n(E) < n_max(E). Отсутствие электрона означает наличие дырки. Тогда число дырок на данном энергетическом уровне или распределение дырок в валентной зоне по энергиям есть разность

(1.3б)

где

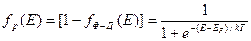(1.4)

− функция распределения дырок.

Во-вторых, пользуясь функцией распределения можно рассчитывать концентрации СНЗ, т.е. количество электронов или дырок в единице объёма, имеющих любое допустимое значение энергии в пределах зоны проводимости и валентной зоны соответственно. Концентрации электронов n и дырок p определяются интегралами

,

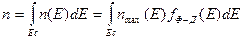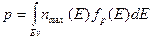(1.5)

где интегрирование следует ограничить областью энергий зоны проводимости (для электронов) и валентной зоны (для дырок).

Наконец, представляется возможным решать обратную задачу: зная концентрацию СНЗ, определять уровень Ферми E_F, и по положению уровня Ферми судить о свойствах полупроводника.

График функции распределения Ферми−Дирака для обозначенных температур приведён на рис. 8.1.

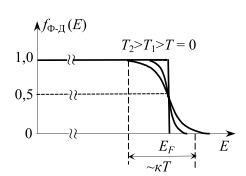
Рис. 8.1. Функция распределения Ферми−Дирака.

• При температуре T = 0 K он представляет собой прямоугольник, площадью . При возрастании температуры освобождаемые площади под кривой распределения в области

E < E_F равны возникающим площадям в области E > E_F. График функции содержит три характерные области:

1). область E < E_F, где

2). область в районе E ≈ E_F протяжённостью в несколько kT, где функция испытывает резкий спад и при E=E_F независимо от температуры равняется ½;

3). область E > E_F, где «на хвосте» распределения при E - E_F > 2kT функцию Ферми−Дирака можно заменить функцией распределения Мак-свелла−Больцмана 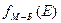. Действительно, пренебрегая единицей в знаменателе (1.2), получим

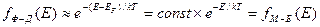(1.6)

• Соотношение (1.1) есть число электронов, приходящихся на одно разрешённое состояние. Очевидно, что всегда 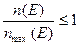Поскольку 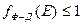то функцию Ферми− Дирака можно рассматривать как вероятность того, что энергетический уровень занят. Тогда число электронов на данном уровне (1.3а) равно произведению максимальной плотности разрешённых состояний на вероятность того, что уровень занят. Функция распределения Ферми−Дирака определяет плотность вероятности занятости состояний с энергией от Е до Е + dE.

• При низких температурах функция Ферми−Дирака равна единице практически вплоть до энергии 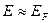, после чего она резко падает. Из вероятностного смысла функции Ферми−Дирака следует, что состояния с энергиями ниже уровня Ферми заняты (вероятность равна 1), а состояния с более высокими энергиями свободны. При повышении температуры определённая часть электронов переходит на более высокие энергетические уровни, значительно (по сравнению с κT) отстоящие от уровня

Ферми, и в области «хвоста» подчиняются статистике Максвелла−Больцмана (1.6) (рис. 8.2). Этот факт является важным результатом, поскольку именно на этих уровнях находятся носители, формирующие токи в полупроводниковых приборах.

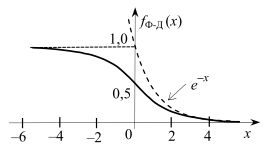
Рис. 8.2. Сравнение функции Ферми−Дирака с экспонентой. На хвосте распределения при 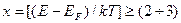функция распределения Ферми−Дирака совпадает с функцией распределения Максвелла−Больцмана.

• Состояния занятого или свободного уровня являются противоположными событиями, сумма вероятностей которых равна 1 как вероятность достоверного события. Поэтому разноость 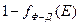дополняющая функцию Ферми−Дирака до единицы, есть вероятность того, что уровень занят дыркой (соотношение (1.4)).

• Распределение дырок в валентной зоне (1.4) выражается такой же формулой, что и распределение электронов (1.2) в зоне проводимости, но с противоположным знаком показателя экспоненты. Это даёт основание направлять ось отсчёта энергии дырок противоположно оси отсчёта энергии электронов (рис. 8.1, рис. 8.3). Тогда во встречно-вложенной системе координат распределение электронов и дырок изображается одной и той же кривой (рис.8.3).

• С точки зрения теории вероятности уровень Ферми определяется как энергетический уровень, вероятность заполнения которого равна точно половине. С точки зрения термодинамики уровень (энергия) Ферми является (в приближении равенства эффективных масс электронов и дырок) химическим потенциалом (в расчёте на один электрон). Химический потенциал используется, в частности, при анализе состояния равновесия в таких гетерогенных (разнородных) системах как, например, жидкость–пар.

Равенство химических потенциалов служит критерием фазового равновесия.

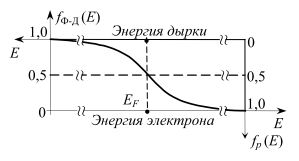
Рис. 8.3. Функция Ферми−Дирака во встречно‐вложенной системе координат.

Оси отсчёта энергии и ординат функций распределения электронов и дырок направлены в противоположные стороны.

Тогда, исходя из термодинамического смысла уровня Ферми, условием электронно-дырочного равновесия в разнородных системах (металлов, полупроводников) является равенство их уровней Ферми во всех частях системы. Единство и постоянство уровня Ферми является необходимым и достаточным условием равновесия электронно-дырочных систем. Сам уровень Ферми определяется из условия, что полное число электронов в кристалле (системе) должно оставаться неизменным вне зависимости от их распределения по энергетическим уровням (ранее упомянутая обратная задача).

Дата добавления: 2014-01-20