Уравнение Шрёдингера

Лекция 9

Энергия электростатического и магнитостатического полей

Рассмотрим влияние энергии одного заряда, находящегося в электростатическом поле.

Пусть под действием сил поля положительный заряд перемещается из точки А в точку В, а затем в точку О, рис. 1.

Рис. 9.1.

В квантовой механике возникает важнейшая проблема об отыскании такого уравнения, которое явилось бы тем же, чем являются уравнения движения Ньютона для классической механики. Как известно, уравнения Ньютона позволяют для макроскопических тел решать основную задачу механики — по заданным силам, действующим на тело (или систему тел), и определенным начальным условиям (начальным значениям координат и скорости тела) найти для любого момента времени координаты тела и его скорость, т. е. описать движение тела в пространстве и во времени. При постановке аналогичной задачи в квантовой механике нужно сразу же учесть, что для частиц микромира характерна двойственная природа, которая ограничивает возможность применения к таким частицам классических понятий о координате и скорости (или импульсе). Вероятностное (статистическое) истолкование волн де Бройля и соотношения неопределенностей указывают, что уравнение движения в квантовой механике должно быть таким, чтобы оно позволяло объяснить наблюдаемые на опыте волновые свойства частиц. Поскольку положение частицы в пространстве в данный момент времени определяется в квантовой механике заданием волновой функции Ψ (х, у, z, t), точнее величиной |Ψ|², определяющей лишь вероятность нахождения частицы в точке х, у, z в момент t, основное уравнение квантовой механики должно быть уравнением относительно функции Ψ (х, у, z, t). Далее, это уравнение должно быть волновым уравнением, ибо из него должны получить свое объяснение эксперименты по дифракции микрочастиц, указывающие на их волновую природу.

Основное уравнение нерелятивистской квантовой механики было найдено в 1926 г. Эрвином Шредингером. Как и уравнения движения Ньютона, лежащие в основе классической механики и поэтому не выводимые, уравнение Шредингера постулируется. Справедливость уравнения Шредингера доказывается тем, что выводы квантовой механики, полученные с помощью этого уравнения в атомной и ядерной физике, находятся в хорошем согласии с опытом. Уравнение Шредингера имеет следующий вид:

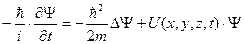(1.1)

Здесь 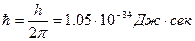- постоянная Планка; m - масса частицы; U (х, у, z, t) - потенциальная энергия частицы в силовом поле, где частица движется; Δ - оператор Лапласа. Оператор - это совокупность действий, которые надо провести над функцией. Оператор Лапласа имеет вид: , Ψ = Ψ (х, у, x, t) — искомая волновая функция частицы; 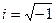мнимая единица.

Рассмотрим составные части уравнения, начиная справа налево.

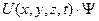- эта часть отражает влияние внешнего потенциального поля на частицы(у) для которых мы составляем уравнение Шредингера.

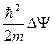- компонента, учитывающая движение рассматриваемых частиц на основе их импульса.

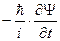- общая форма записи волнового уравнения. Указывает на то, что движение рассматриваемых частиц имеет волновую природу, а следовательно должно описываться волновым уравнением.

Уравнение (1.1) справедливо для любой частицы, движущейся со скоростью v<<c (с — скорость света в вакууме). В релятивистской области при v ≈ c уравнение Шредингера заменяется более сложным релятивистским уравнением Дирака.

Шредингер, в качестве возможного вида функции 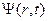, удовлетворяющих уравнению (1.1), предложил следующий вид функций:

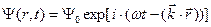
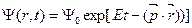(1.2)

ω - круговая частота, k - волновое число, Е – энергия частицы, р – её импульс.

Уравнение (1.1) часто называют временным уравнением Шредингера, ибо оно содержит производную от функции Ψ по времени. Однако для большого числа физических явлений, происходящих в микромире, например для описания поведения электрона в атоме, в ряде случаев важно уметь находить стационарные решения уравнения Шредингера, не содержащие времени. Для решения этой задачи нужно получить так называемое стационарное уравнение Шредингера, в котором исключена зависимость Ψ от времени. Оно имеет смысл для тех задач, в которых потенциальная энергия U не зависит от времени: U = U (х, у, z). Будем искать решение уравнения (1.1) в виде произведения двух функций:

(1.3)

в котором разделены переменные: ψ является функцией только координат, ϕ -

функцией только времени. Подставляя (1.3) в (1.1) и производя дифференцирование,

получаем:

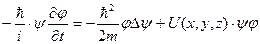
Разделим правую и левую части уравнения на произведение ψ⋅ϕ:

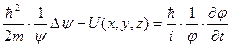(1.4)

Поскольку левая часть уравнения есть функция только координат, а правая - функция только времени, уравнение (1.4) удовлетворяется при единственном условии - обе части равны постоянной величине. Обозначим ее через (-W):

(1.5)

(1.6)

Уравнение (21.6) обычно записывают в форме:

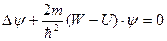(1.7)

и называют стационарным уравнением Шредингера. Разность (W – U) имеет смысл кинетической энергии частицы, а W – её полной энергии.

Уравнение (1.7) является важнейшим соотношением нерелятивистской квантовой механики, играющим основную роль в атомной физике. Функции ψ, удовлетворяющие уравнению Шредингера при данном значении U, называются собственными функциями. Значения W, при которых существуют решения уравнения Шредингера (1.7), называются собственными значениями.

Дата добавления: 2014-01-20