Уравнения Максвелла для электростатических и магнитостатических полей

Ранее было установлено, что

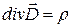или .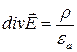

Так как электростатическое поле является потенциальным, то 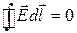и

.

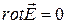Пару уравнений

,

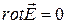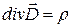(9.2)

называют уравнениями Максвелла, описывающими постоянные электростатические поля.

Пусть требуется решить прямую задачу определения напряженности поля по заданному распределению параметров.

Учитывая, что напряженность поля 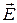связана с его потенциалом 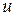уравнением

,

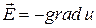которое здесь получаем формально из (9.1), т.к. 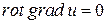(см. (8.11)) и, подставляя это формально в уравнение (9.2), получим уравнение Пуассона

,

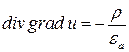или

.

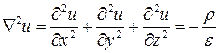Решением этого уравнения будет равенство

.

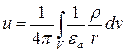Тогда

.

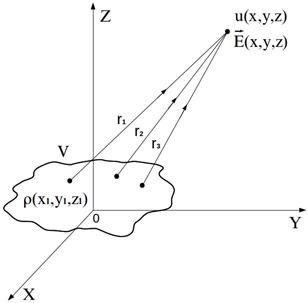
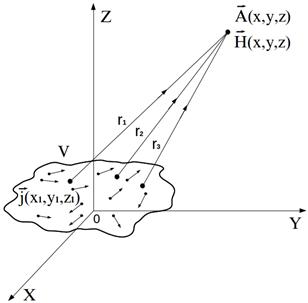
Рис. 9.1.

Так как переменные наблюдения 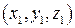, рис. 9.1, и переменные интегрирования 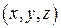– это различные переменные (хотя и относятся к одной и той же системе координат), то операцию градиента как операцию дифференцирования по параметру, не совпадающему с переменной интегрирования, можно внести под знак интеграла. Тогда

.

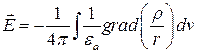На примере использования функций одной переменной это выглядит так:

.

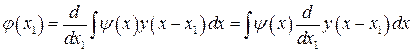Если наблюдение поля 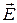осуществляется в тех точках пространствах, где отсутствуют заряды, то

.

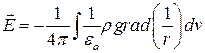Так как

,

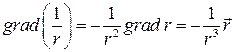где

,

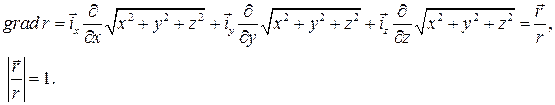В операторном виде:

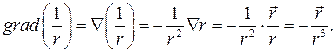
Так как функция является возрастающей функцией и обладает сферической симметрией, то направления векторов 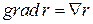положительны и совпадают с направлениями .

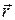Тогда напряженность електростатического поля в тех точках, в которых отсутствуют заряды, рассчитывается по формуле:

.

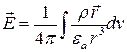Для точечного заряда

.

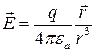Таким образом, здесь закон Кулона получен как решение уравнений Максвелла (9.1), (9.2). Заметим, что здесь все выкладки осуществлялись уже формально математически в процессе решения системы уравнений Максвелла.

Рассмотрим теперь по аналогии уравнения Максвелла и их решение для магнитостатического поля.

Этими уравнениями являются уже полученные нами соотношения

,

.

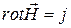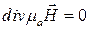Первое уравнение говорит о том, что роторами (вихрями) поля являются плотности токов, вокруг которых замыкаются линии магнитного поля. Второе уравнение свидетельствует о замкнутости линий магнитного поля, т.е. об их соленоидальном характере, а также об отсутствии магнитных зарядов.

Это дифференциальное уравнение в частных производных, неизвестными в которых при заданных 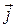являются компоненты вектора магнитного поля 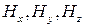. Рассмотрим методику их нахождения, т.е. методику решения этих уравнений.

На основании формулы 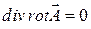(см. (8.13) и (9.13)) запишем

.

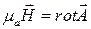Это позволяет найти компоненты поля 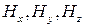после предварительного определения составляющих вектора 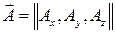. Этот вектор называют векторным потенциалом поля.

Так как поле 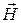соленоидальное (вихревое), то вектор 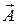также удовлетворяет условию

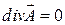
(так как в соленоидальном поле нет ни для 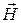, ни для 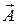, ни стоков, ни истоков).

Уравнение (9.12) с учетом(9.14) примет вид:

.

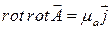На основании (8.15)

.

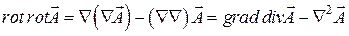Тогда имеем,

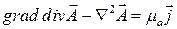. (9.16)

Первое слагаемое равно нулю на основании (9.15). Тогда компоненты векторного потенциала можно найти из дифференциального уравнения

.

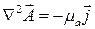В координатной форме это уравнение запишется так:

, , .

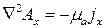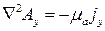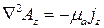Каждое из этих уравнений внешне подобно уравнению для скалярного потенциала (9.3). Подобными будут и решения

, , .

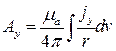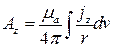В векторной форме эти уравнения примут вид:

.

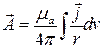Таким образом, найдем векторный потенциал поля 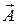. Само поле 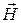, учитывая, что 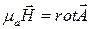находим по формуле

.

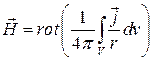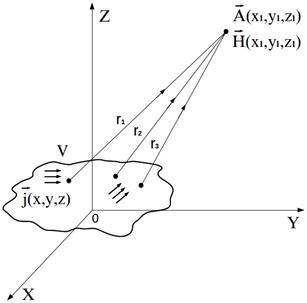
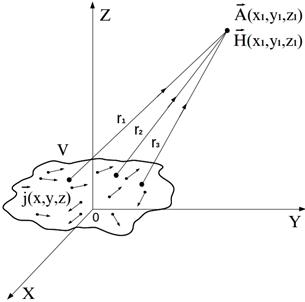
Рис. 9.2.

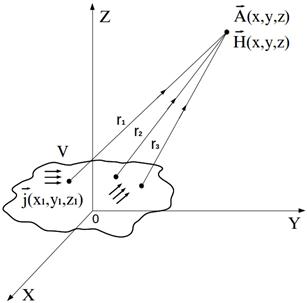
Также как и в формулах (9.5) и (9.7) здесь следует различать переменные наблюдения (координаты 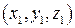) и переменные интегрирования (такие же координаты 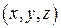, но соответствующим другим точкам пространства в объеме 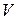, рис.9.2). Тогда оператор ротора, как дифференциальный оператор, действующий по переменным наблюдения можно внести под знак интеграла как производную по параметру. В результате получим

.

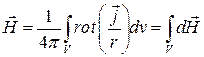На основании формулы (см. (8.20))

.

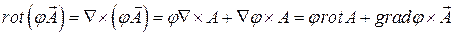
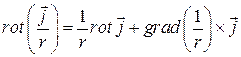Полагая, что в точках наблюдения токи отсутствуют, т.е. 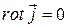(операция, которая осуществляется для поля по переменным наблюдения), а также учитывая, что

,

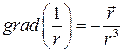получим

,

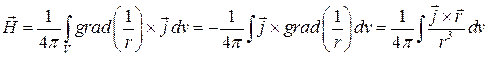где

,

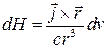что соответствует закону Био-Савара.

Заметим, что этот закон уже не постулирован, как ранее, а выведен математически, как результат решения системы уравнений Максвелла (9.12) и (9.13).

Дата добавления: 2014-01-20