Неинерциальные системы отсчета. Силы инерции

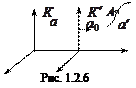Законы динамики в неинерциальных системах отсчета можно применять, если кроме сил, обусловленных взаимодействием тел друг на друга, ввести в рассмотрение силы особого рода – силы инерции.

Пусть 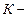инерциальная система отсчета. Тогда урав-

нение движения тела 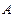в этой системе 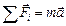. Сис-

тема 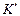- неинерциальная, т.к. движется относитель-

но системы 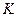с ускорением 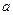, т.е. в системе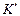

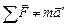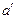(— ускорение тела в системе отсчета 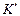и 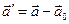). Для того чтобы уравнение движения в форме второго закона Ньютона можно было использовать и в неинерциальных системах (в нашем случае система 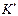) вводят силы особого рода – силы инерции 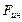. Эти силы не связаны взаимодействием тел, а обусловлены ускоренным движением системы отсчета. Тогда уравнение движения тела 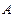в системе 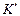будет иметь вид 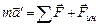. Вычитая из него уравнение 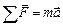, найдем 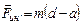(1.2.11)

Второй закон Ньютона в этом случае: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции). Силы инерции вызываются не взаимодей­ствием тел, а ускоренным движением системы отсчета. Силы инерции 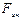должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а', каким оно обладает в неинерциальных системах отсчета.

Силы инерции обусловлены ускорен­ным движением системы отсчета относи­тельно измеряемой системы, поэтому в об­щем случае нужно учитывать следующие случаи проявления этих сил: силы инер­ции т. е.

1) при ускоренном поступательном дви­жении системы отсчета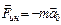 (1.2.12)

Например, когда автомобиль набирает ско­рость, то пассажир под действием силы инерции прижимается к спинке сиденья. Наоборот, при торможении автомобиля сила инерции направлена в противоположную сторо­ну и пассажир отделяется от спинки сиденья. Особенно эти силы заметны при внезапном тор­можении. Силы инерции проявляются в перегрузках, которые возникают при запуске и торможении космических кораблей.

Дано:    

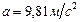Пример 1.2.7. К потолку вагона, движущегося в горизонтальном направлении с ускорением , подвешен на нити шарик массой 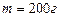. Определите для установившегося движения: 1) силу натяжения нити 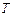; 2) угол 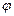отклонения нити от вертикали.

Решение:

Рис. 1.2.7

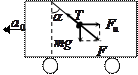
При равномерном прямолинейном движении на шар действуют уравновешивающие друг друга силы тяжести и натяжения нити. Пусть ускорение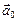

вагона направлено в ту же сторону, что и скорость вагона 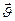. Т.к. вагон идет с ускорением, то шар отстает от него, т.е. относительно системы отсчета, связанной с вагоном, шар приобрел ускорение -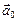и 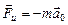. Это фиктивная сила, которую приходится вводить в ускоренной системе отсчета, чтобы в ней выполнялся II закон Ньютона – сила инерции. Ее величина 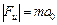. Результирующая сила 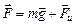, ее величина 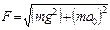, т.к. шарик находится в равновесии, то ,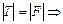

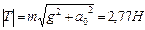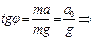
Дата добавления: 2014-01-11