Установившийся режим

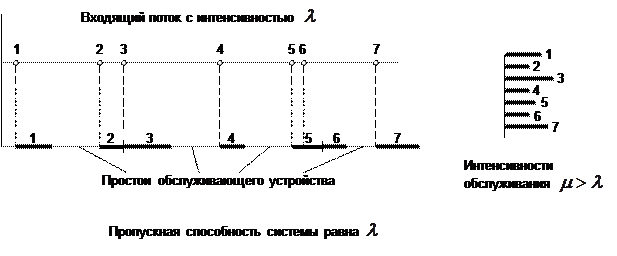
Режимы работы СМО M/M/1

III. Заключительные положения

18. Журналы, указанные в пунктах 13 и 15, могут вестись в электронном и (или) письменном виде.

В электронном виде журналы ведутся с использованием комплекса программных средств автоматизированных систем контроля за таможенным транзитом, включенных в фонд алгоритмов и программных средств ФТС России.
В письменном виде журналы формируются путем распечатки данных электронных журналов в форме отдельных листов по окончании каждого рабочего дня (смены) либо последнего рабочего дня недели (в зависимости от количества принимаемых транзитных деклараций), которые подшиваются в отдельный журнал с описью подшитых листов. Каждый лист распечатки данных пронумеровывается, вносится в опись с указанием даты составления распечатки и количества оформленных транзитных деклараций, заверяется подписью и оттиском личной номерной печати должностного лица таможенного органа, ответственного за ведение журналов.

Формула Литтла. Теперь мы выведем одну важную формулу, связывающую (для предельного стационарного режима) среднее число заявок 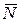, находящихся в системе массового обслуживания (т.е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе 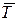. Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или ограниченной очередью) и связанные с ней два потока событий: поток заявок, прибывающих в СМО, и поток заявок покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность .

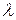Обозначим: 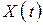– число заявок, прибывших в СМО до момента 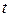, 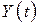– число заявок, покинувших СМО до момента 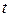. И та, и другая функция являются случайными и меняются скачком (увеличиваются на единицу) в моменты прихода заявок 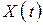и уходов заявок 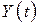. Вид функци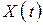й и 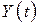показан на рисунке.

Обе линии – ступенчатые, верхняя – 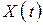, нижняя – 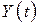. Очевидно, что для любого момента 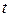их разность 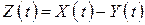есть не что иное, как число заявок, находящихся в СМО. Когда лини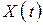и и 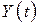сливаются, в системе нет заявок.

Рассмотрим очень большой промежуток времени 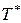(мысленно продолжив график далеко за пределы чертежа) и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции 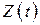на этом промежутке, деленному на длину интервала :

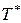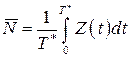. (1)

Но этот интеграл представляет собой не что иное, как площадь фигуры, заштрихованной на рисунке. Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т.д.). Обозначим эти времена 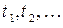. Правда, под конец промежутка 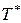некоторые прямоугольники войдут в заштрихованную фигуру не полностью, а частично, но при достаточно большом 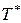эти мелочи не будут играть роли. Таким образом, можно считать, что

, (2)

где сумма распространяется на все заявки, пришедшие за время .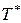

Разделим правую и левую части (2) на длину интервала 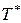. Получим с учетом (1),

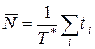. (3)

Разделим и умножим правую часть (3) на интенсивность l:

.

Но величина 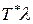есть не что иное, как среднее число заявок, пришедших за время 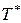. Если мы разделим сумму всех времен 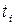на среднее число заявок, то получим среднее время пребывания заявки в системе 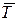. Итак

,

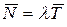Откуда

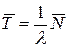. (4)

Это и есть формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.

Точно таким же образом выводится вторая формула Литтла, связывающая время пребывания заявки в очереди 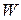с среднее число заявок в очереди :

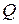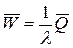. (5)

Для вывода достаточно вместо нижней линии на рисунке взять функцию – количество заявок, ушедших до момента 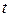не из системы, а из очереди (если заявка, пришедшая в систему, не становится в очередь, а сразу идет под обслуживание, можно все же считать, что она становится в очередь, но находится в ней нулевое время).

Дата добавления: 2014-01-20