
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение движения твердого тела, вращающегося вокруг неподвижной оси
|
|
|
|
Если тело вращается вокруг неподвижной оси, то по (1.4.3.) 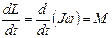 . Если тело абсолютно твердое, то
. Если тело абсолютно твердое, то 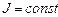 , т.к. в процессе движения форма и размеры тела не изменяются и
, т.к. в процессе движения форма и размеры тела не изменяются и 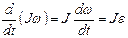 , откуда получим выражение, связывающее момент силы и момент инерции:
, откуда получим выражение, связывающее момент силы и момент инерции:  (1.4.10)
(1.4.10)
- основное уравнение динамики вращательного движения (при описании вращательного движения играет такую же роль, второй закон Ньютона при поступательном).
Выражение (1.4.10) можно получить, если в формуле (1.4.2”)ввести замену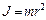 .
.
Из полученного соотношения видно, что момент инерции тела характеризует инерциальные свойства тела при вращательном движении (такие как масса при поступательном). Мы получили, что угловое ускорение 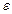 таким же образом связано с моментом силы
таким же образом связано с моментом силы 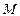 и моментом инерции
и моментом инерции 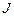 , каким тангенсальное ускорение
, каким тангенсальное ускорение 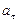 связано с силой
связано с силой  и массой
и массой  точки. При таком описании вращательного движения роль силы играет момент силы, роль массы – момент инерции. Т.о., материальные точки с разными массами эквивалентны в смысле приобретаемого ими углового ускорения, если равны их моменты инерции.
точки. При таком описании вращательного движения роль силы играет момент силы, роль массы – момент инерции. Т.о., материальные точки с разными массами эквивалентны в смысле приобретаемого ими углового ускорения, если равны их моменты инерции.
а) в общем случае: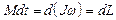 , (1.4.10)
, (1.4.10)
где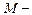 момент силы, действующей на тело в течение времени
момент силы, действующей на тело в течение времени 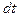 ,
,  момент импульса;
момент импульса;
б) в случае постоянных момента силы и момента инерции 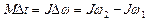 ; (1.4.11)
; (1.4.11)
в) в случае постоянного момента инерции 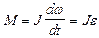 (1.4.12)
(1.4.12)
г) уравнение динамики тела, вращающегося относительно оси OZ 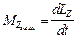 , где
, где 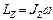 и
и 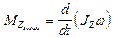 - проекции моментов импульса и внешних сил на ось вращения.
- проекции моментов импульса и внешних сил на ось вращения.
Пример 1.4.6. Тонкий стержень длиной 50 см и массой 400 г вращается с угловым ускорением 3 рад/с2 около оси, проходящей через середину стержня перпендикулярно к его длине. Определить вращающий момент М.
Решение:  ;
;  ;
; 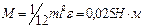
 Пример 1.4.7. Вал в виде сплошного цилиндра массой 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой 2 кг. С каким ускорением будет опускаться гиря, если ее предоставить самой себе?
Пример 1.4.7. Вал в виде сплошного цилиндра массой 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой 2 кг. С каким ускорением будет опускаться гиря, если ее предоставить самой себе?
Решение: Равнодействующая сил  и
и 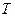 вызывает равноускоренное движение гири
вызывает равноускоренное движение гири 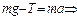
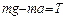 ;
; 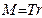 ;
; 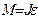 ;
;  ;
; 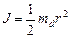 ;
;  ;
; 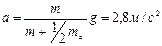
Пример 1.4.8. Вал массой 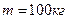 и радиусом
и радиусом  вращался с частотой
вращался с частотой 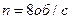 . К цилиндрической поверхности вала прижали тормозную колодку с силой
. К цилиндрической поверхности вала прижали тормозную колодку с силой 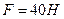 , под действием которой вал остановился через
, под действием которой вал остановился через  . Определить коэффициент трения.
. Определить коэффициент трения.
Решение:
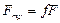 ,
, 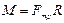 ,
,  ,
,  ,
, 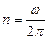
 и
и 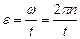 .Получаем
.Получаем 
Пример 1.4.9. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение оси цилиндра, если цилиндр а) сплошной; б) полый, тонкостенный.
Решение: Равнодействующая сил  и
и 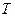 вызывает равноускоренное движение цилиндра
вызывает равноускоренное движение цилиндра 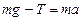 ;
;  ;
;  ;
; 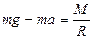 ;
;
1)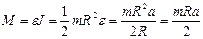 ;
; 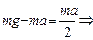
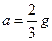 ;
;
2) 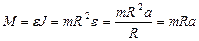 ;
; 


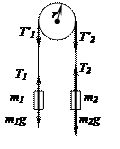 Пример 1.4.10. Через блок в виде диска, имеющего массу 80 кг, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами 100 кг и 200 кг. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Пример 1.4.10. Через блок в виде диска, имеющего массу 80 кг, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами 100 кг и 200 кг. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
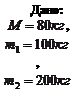 Решение:
Решение:

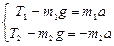 ;
;  ;
; 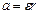 ;
; 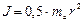 ;
; 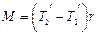 ;
;
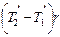
 ;
; 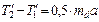 . Т.к.
. Т.к. и
и  , то
, то 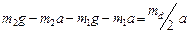 , откуда
, откуда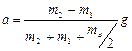 .
.
Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется – фундаментальный закон, связан со свойством симметрии пространства – его изотропностью.
а) в общем виде 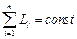 , (1.4.13)
, (1.4.13)
где 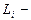 момент импульса тела с номером
момент импульса тела с номером  , входящего в состав системы;
, входящего в состав системы;
б) для двух тел 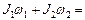
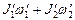 , где
, где  моменты инерции и угловые скорости тел до взаимодействия,
моменты инерции и угловые скорости тел до взаимодействия, 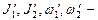 те же величины после взаимодействия;
те же величины после взаимодействия;
в) для однородного тела, момент инерции которого может
 меняться
меняться  , где
, где 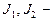 начальное и конечное значения момента инерции,
начальное и конечное значения момента инерции,  начальная и конечная угловые скорости тела.
начальная и конечная угловые скорости тела.
 Сохранение момента количества движения может быть продемонстрировано с помощью человека, стоящего на скамеечке, которая может без трения вращаться вокруг вертикальной оси («скамья Жуковского»). Пусть человек стоит на такой скамеечке и держит в расставленных руках гири. Скамеечка вместе с человеком вращается с угловой скоростью
Сохранение момента количества движения может быть продемонстрировано с помощью человека, стоящего на скамеечке, которая может без трения вращаться вокруг вертикальной оси («скамья Жуковского»). Пусть человек стоит на такой скамеечке и держит в расставленных руках гири. Скамеечка вместе с человеком вращается с угловой скоростью 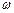 . При этом человек имеет определенный момент количества движения
. При этом человек имеет определенный момент количества движения 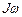 , который должен сохраниться при равенстве нулю момента внешних сил. Если человек опустит руки, то его момент инерции уменьшится, в результате чего возрастет угловая скорость его вращения
, который должен сохраниться при равенстве нулю момента внешних сил. Если человек опустит руки, то его момент инерции уменьшится, в результате чего возрастет угловая скорость его вращения 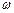 . Если человек снова поднимет руки, то угловая скорость
. Если человек снова поднимет руки, то угловая скорость 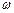 снова примет прежнее значение.
снова примет прежнее значение.
Пример 1.4.4. Человек стоит на скамейке Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки. Скамейка с человеком вращается с частотой  . С какой частотой будет вращаться скамейка, если человек повернет стержень так, чтобы он принял горизонтальное положение? Суммарный момент инерции человека и скамейки
. С какой частотой будет вращаться скамейка, если человек повернет стержень так, чтобы он принял горизонтальное положение? Суммарный момент инерции человека и скамейки 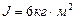 , длина стержня
, длина стержня  , его масса
, его масса 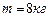 .
.

|

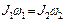 , где
, где  и
и 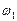 - момент инерции тела человека и угловая скорость скамейки и человека с вертикальным стержнем,
- момент инерции тела человека и угловая скорость скамейки и человека с вертикальным стержнем,  и
и  - момент инерции тела человека и угловая скорость скамейки и человека с горизонтальным стержнем.
- момент инерции тела человека и угловая скорость скамейки и человека с горизонтальным стержнем. 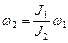 .
. 
 .
.
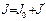 , где
, где  моменты инерции человека и стержня в руках человека.
моменты инерции человека и стержня в руках человека. 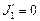 ,
, 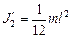 . Получаем
. Получаем 
Ответ: 
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1278; Нарушение авторских прав?; Мы поможем в написании вашей работы!
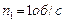 ,
, ,
, 