
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энергия
|
|
|
|
Т.к. кинетическая энергия поступательного движения материальной точки определяется формулой 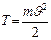 , то, учитывая формулу
, то, учитывая формулу 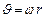 , можно найти аналогичное выражение для кинетической энергии вращательного движения. Для материальной точки, вращающейся вокруг некоторой оси, получим
, можно найти аналогичное выражение для кинетической энергии вращательного движения. Для материальной точки, вращающейся вокруг некоторой оси, получим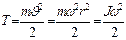 , (1.4.14)
, (1.4.14)
где 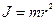 – момент инерции материальной точки относительно оси вращения.
– момент инерции материальной точки относительно оси вращения.
Кинетическая энергия твердого тела, совершающего вращательное движение 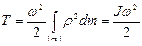 ,
,
где J – момент инерции тела относительно оси вращения.
Если тело совершает вращательное и поступательное движения(например, катится по плоскости без скольжения), то его полная кинетическая энергия может быть представлена в виде суммы энергий поступательного и вращательного движений 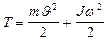 (1.4.15) где
(1.4.15) где  скорость центра инерции тела;
скорость центра инерции тела;  – момент инерции тела, относительно оси, проходящей через центр инерции.
– момент инерции тела, относительно оси, проходящей через центр инерции.
Найдем работу момента силы, действующего на вращающееся тело. Пусть тело вращается вокруг неподвижной оси. Сила, приложенная к к некоторой точке тела, совершает элементарную работу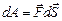 , где
, где 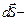 перемещение этой точки за малое время.
перемещение этой точки за малое время. 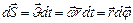 , где
, где 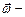 угловая скорость точки,
угловая скорость точки, 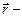 расстояние от центра окружности до точки приложения силы,
расстояние от центра окружности до точки приложения силы,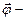 угол поворота тела. По формуле (1.4.1)
угол поворота тела. По формуле (1.4.1) 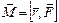 , и получаем
, и получаем 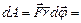
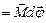 . Или работа постоянного момента силы
. Или работа постоянного момента силы 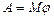 , (1.4.16)
, (1.4.16)
Работа, совершаемая при вращении тела, и изменение кинетической энергии его связаны соотношением 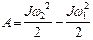 . (1.4.17)
. (1.4.17)
Мгновенная мощность, развиваемая при вращении тела
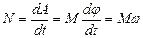 (1.4.18)
(1.4.18)
Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения.
| Поступательное движение | Вращательное движение |
| Основные понятия | |
масса 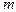
| момент инерции 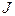
|
скорость 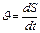
| угловая скорость 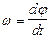
|
ускорение 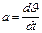
| угловое ускорение 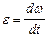
|
сила 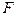
| момент силы 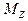 или или 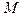
|
импульс 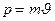
| момент импульса 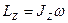
|
| Основной закон динамики (второй закон Ньютона) | |
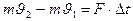
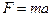
| 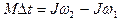
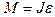
|
| Закон сохранения | |
импульса: 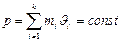
| момента импульса: 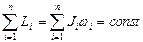
|
| Работа и мощность | |
 , , 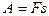
| 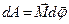 , , 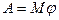
|
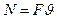
| 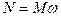
|
| Кинетическая энергия | |
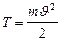
| 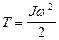
|
| Условия статического равновесия тела (системы тел) | |
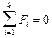
| 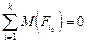
|
| Уравнения движения | |
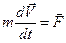 , , 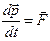
| 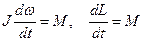
|
Пример 1.4.11. Какую часть от общей кинетической энергии составляет энергия вращения для катящихся: 1) обруча; 2) сплошного цилиндра; в) шара.
Решение: 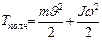
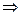
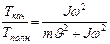 , т.к.
, т.к. 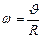 , то
, то 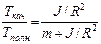 . 1) Для обруча
. 1) Для обруча 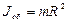
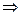
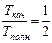 2) Для сплошного цилиндра
2) Для сплошного цилиндра 
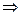
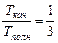 ; 3) Для шара
; 3) Для шара 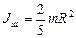
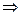
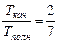 .
.
Пример 1.4.12. С наклонной плоскости высотой  скатываются: 1) обруч; 2) сплошной цилиндр; 3) шар. Найти поступательные скорости, которые они будут иметь, скатившись до конца плоскости. Сравнить эти скорости со скоростью, которое имело бы тело, соскальзывающее по плоскости без трения.
скатываются: 1) обруч; 2) сплошной цилиндр; 3) шар. Найти поступательные скорости, которые они будут иметь, скатившись до конца плоскости. Сравнить эти скорости со скоростью, которое имело бы тело, соскальзывающее по плоскости без трения.
Решение: В отсутствии трения систему можно считать замкнутой. Каждое из тел в начальный момент времени обладает потенциальной энергией 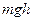 , которая затем преобразуется в кинетическую энергию поступательного движения
, которая затем преобразуется в кинетическую энергию поступательного движения 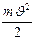 и кинетическую энергию вращения
и кинетическую энергию вращения 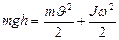 . Т.к.
. Т.к. 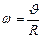 , то
, то 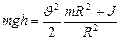
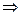
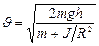 . Для тела, соскальзывающего без трения с наклонной плоскости,
. Для тела, соскальзывающего без трения с наклонной плоскости, 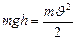 , откуда
, откуда 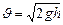 . 1) Для обруча
. 1) Для обруча 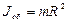 ,
,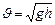 ; 2) Для сплошного цилиндра
; 2) Для сплошного цилиндра  ,
,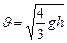 ; 3) Для шара
; 3) Для шара 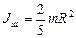
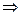
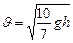 .
.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1207; Нарушение авторских прав?; Мы поможем в написании вашей работы!