Энергия колебаний

Кинетическая энергия

Потенциальная энергия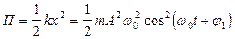

Полная энергия колеблющейся точки 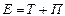. Кинетическая энергия имеет нуль там, где потенциальная достигает максимума, т.е. в положениях крайнего отклонения; кинетическая энергия достигает максимума при прохождении положения равновесия, потенциальная энергия в этой точке равна нулю. 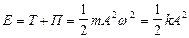. В точках крайнего смещения вся энергия переходит в потенциальную, при прохождении положения равновесия вся энергия переходит в кинетическую.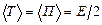

Гармонические колебания изображаются графически методом векторных диаграмм.

Пример 2.2.1. Какова частота, амплитуда и начальная фаза колебаний, заданных уравнением , см. Каковы максимальная скорость и ускорение точки, колеблющейся по заданному закону?

Решение:

По условию задачи , см. Следовательно, ; ; ; ; . .

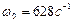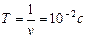Пример 2.2.2. Материальная точка массой 400 г совершает гармонические колебания вдоль горизонтальной оси 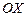по закону 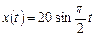. Найти силу, действующую на точку.

Решение:

Найдем проекцию ускорения колеблющейся точки на ось ОХ: 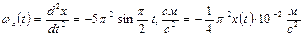. Проекция действующей силы на ось ОХ: . Т.к. проекция силы на ось ОХ и координата колеблющейся точки противоположны по знаку, то сила направлена к началу координат, т.е. играет роль возвращающей силы.

Пример 2.2.3. Материальная точка массой совершает гармонические колебания с частотой . Амплитуда колебаний . Определить: 1) скорость точки в момент времени, когда смещение 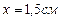; 2) максимальную силу, действующую на точку; 3) полную энергию колеблющейся точки.

Решение:

1); . Чтобы выразить скорость через смещение, надо исключить из данных формул время.

, . Возведем оба уравнения в квадрат и сложим 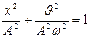или . Решив данное уравнение относительно 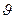, найдем 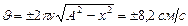. Знак «плюс» соответствует случаю, когда направление скорости совпадает с положительным направлением ОХ. Знак «минус» соответствует случаю, когда направление скорости совпадает с отрицательным направлением ОХ.

2) , , , , .

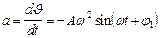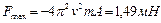3) полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени.

Опр. 2.2.3. Гармоническим осциллятором наз. система, совершающая колебания, описываемые уравнением.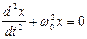

Колебания гармонического осциллятора являются важным примером периодического движения и служат моделью во многих задачах физики. Примерами гармонического осциллятора являются маятники.

Дата добавления: 2014-01-11