Волновые процессы

Если рассматривается сплошная среда, то в ней могут распространяться колебания. Процесс распространения колебаний называется волной или волновым процессом. Волны можно разделить на продольные и поперечные.

Волны называются поперечными, если частицы среды смещаются в направлении перпендикулярном направлению распространения волны.

Примерами поперечных волн являются волны на поверхности воды, электромагнитные волны, упругие волны, распространяющиеся в твердых телах.

Волны называются продольными, если частицы среды смещаются в направлении распространения волны.

Для плотности среды в продольных волнах получается периодическая функция (сжатие – растяжение). Примеры продольных волн: распространение звука, внутренние волны в твердых, жидких и газообразных телах.

Отметим, что при распространении волны частицы среды совершают периодические колебания. Поэтому волны и колебательные процессы связаны между собой и имеют много общего. Введем основные характеристики волновых процессов.

Длиной волны называется расстояние между ближайшими частицами, колеблющимися в одинаковой фазе (одинаковым образом). Если частица среды колеблется с периодом Т, а скорость распространения волны u, то между длиной волны λ, периодом Т и скоростью распространения волны 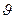существует связь .

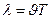Вместо периода колебаний часто используют частоту 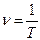, которая равна числу колебаний точки среды за единицу времени.

При распространении волны частицы среды не переносятся волной, а лишь совершают колебания. Волной переносится энергия и импульс.

Волновым фронтом называется геометрическое место точек, до которых доходят колебания к рассматриваемому моменту времени. Пример: распространение волны на поверхности воды от брошенного камня.

Волновой поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе. Волновые поверхности могут иметь различную форму: плоские, цилиндрические, сферические и др.

Рассмотрим плоскую волну, которая распространяется вдоль оси х. Если смещение точек среды обозначить ξ(x,t), то распространяющаяся волна описывается уравнением .

Это уравнение называют уравнением бегущей волны. Здесь А – амплитуда волны, – циклическая частота волны, 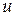– скорость распространения волны. Часто для характеристики распространяющейся волны используют волновое число,которое является величиной, обратной длине волны: ,

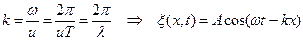Для описания волновых процессов можно получить специальное дифференциальное уравнение в частных производных (волновое уравнение ), которое значительно сложнее, чем уравнение колебаний.

Распространение звука, света, электромагнитного излучения описывается в рамках теории волновых процессов. При распространении и взаимодействии волн возникает много явлений, которые не имеют аналогов в механике: интерференция, дифракция, дисперсия, поляризация и др.

Скорость распространения волны 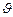, длина волны 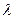, частота 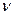(или период 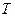) связаны соотношениями: , .

Уравнение бегущей волны 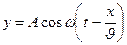, где 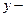смещение точки, имеющей координату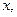 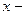расстояние точки от источника колебаний (координата).

Пример 12. Поперечная волна распространяется вдоль упругого шнура со скоростью 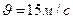. Период колебаний точек шнура 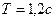, амплитуда 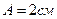. Определить: 1) длину волны 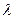; 2) фазу колебаний, смещение, скорость и ускорение точки, отстоящей на расстоянии от источника волн в момент времени 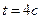; 3) разность фаз колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях и .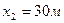

Решение:

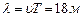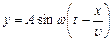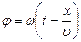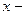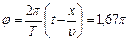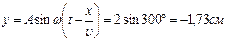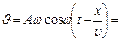
. Фаза-выражение, стоящее под знаком синуса: , где расстояние точки от источника волн. . . . . 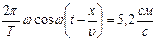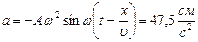Разность фаз .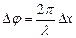

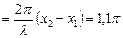Дата добавления: 2014-01-11