Определение

При наличии п наблюдений двух переменных (х и у) выборочная ковариация между ними задается формулой

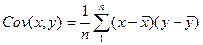1.

Для различения ковариаций выборочной и генеральной совокупностей мы будем использовать обозначение Cov (x,y) c прописной буквы С применительно к выборочной ковариации и рор. соv (x,y) - для ковариации между х и у в генеральной совокупности. Иногда последнюю будет удобно обозначать как s_ху. Аналогичные обозначения мы используем и для дисперсии: Var (x) - применительно к выборочной дисперсии и рор.var (x) - к дисперсии для генеральной совокупности (теоретической).

Таблица 1.1

Наблюдения	р	у	z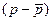
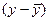
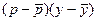
	103,5	26,2	865,3	-39,86	-0,07	2,79
	127,0	24,8	858,4	-16,36	-1,47	24,05
	126,0	25,6	875,8	-17,36	-0,67	11,63
	124,8	26,8	906,8	-18,56	0,53	-9,84
	124,7	27,7	942,9	-18,66	1,43	-26,68
	121,6	28,3	988,8	-21,76	2,03	-44,17
	149,7	27,4	1015,5	6,34	1,13	7,16
	188,8	25,1	1021,6	45,44	-1,17	-53,16
	193.6	25,2	1049,3	50,24	-1,07	-53,76
	173,9	25,6	1058,3	30,54	-0,67	-20,46
Сумма	1433,6	262,7	9582,7	х	х	-162,44
Среднее	143,36	26,27	958,2	х	х	-16,24

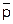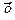В примере с бензином вы должны заметить, что ковариация отрицательна. Так и должно быть. Рассмотрим причину этого. Диаграмма рассеяния наблюдений на рис.1.1 делится на четыре части вертикальной и горизонтальной линиями, проведенными через и соответственно. Пересечение этих линий образует точку, которая показывает среднюю цену и средний спрос за период времени, соответствующий нашей выборке. Используя аналогию из физики, можно сказать, что эта точка является центром тяжести совокупности точек, представляющих наблюдение.

Для любого наблюдения, лежащего в квадранте А, значения реальной цены и спроса выше соответствующих средних значений. Для данных наблюдений как (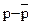), так и 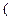у- 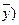являются положительными, а поэтому положительно и произведение этих наблюдений. Таким образом, наблюдения в квадранте А дают положительный вклад в ковариацию.

Далее рассмотрим квадрант В. Здесь наблюдения имеют реальную цену ниже среднего, а спрос выше среднего. Поэтому наблюдения данного квадранта вносят отрицательный вклад в ковариацию. В квадранте С как цена, так и спрос ниже своих средних значений, поэтому отклонения этих переменных от своих средних будут отрицательны, а их произведение - положительно. Наконец, в квадранте D реальная цена выше средней, а спрос выше среднего и можно понять, что квадрант D вносит отрицательный вклад в ковариацию.

Поскольку выборочная ковариация является средней величиной произведения (р-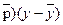 для 10 наблюдений, она будет положительной, если положительные вклады будут доминировать над отрицательными и отрицательной, если отрицательные вклады будут доминировать над положительными. Положительные вклады исходят из квадрантов А и С, и ковариация будет, скорее всего, положительной, если основной разброс пойдет по наклонной вверх. Точно также отрицательные вклады исходят из квадрантов B и D. Поэтому, если основное рассеяние идет по наклонной вниз, как в этом примере, то ковариация будет, скорее всего, отрицательной.

1.3. Основные правила расчета ковариации.

Есть несколько важных правил, которые вытекают непосредственно из определения ковариации.

Правило 1.

Если у = а + в, то Cov (x,y) = Cov (x,а) + Cov (x, в) 2.

Доказательство правила 1

(x - 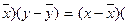а + в - 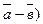= (х -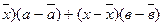

Таким образом, мы доказали, что Соv (х,у) является суммой ковариаций Cov (x,a) и Cov (x,в).

Это правило можно пояснить на следующем примере. Допустим, х - доход семьи, у - расходы на питание и одежду, которые в свою очередь можно разбить на а - расходы на питание и в - расходы на одежду. Тогда, согласно правилу 1, ковариация доходов с общими расходами (у) может быть определена как сумма ковариации доходов с расходами на питание (а) и ковариации доходов с расходами на одежду (в).

Правило 2

Если у = к с, где к - константа, то Cov (х, у) = к Cov (х,с) 3.

Доказательство правила 2

Cov (x, y) = = =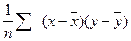

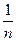
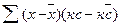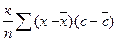= к Cov (x,c)

Правило 3

Если у = а, где а - константа, то Cov (х,у) = 0. 4.

Доказательство правила 3

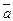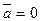
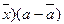Это совсем просто. Поскольку а - константа, то = а. Отсюда а - и, следовательно, (х - =0. Поэтому Cov (х, а) = 0.

Пользуясь этими основными правилами, вы можете упрощать значительно более сложные выражения с ковариациями. Например, если какая то переменная равна сумме трех переменных - u, v и w, то, пользуясь правилом 1 и разбив у на две части (u и v + w), получим:

Cov (x, y) = Cov (x, u + v + w) = Cov (x, u) + Cov (x, v + w) = Cov (x,u) + Cov (x, v) + Cov (x, w).

Итак, выборочная ковариация между х и у определяется по формуле 1.1. Другим эквивалентным выражением является

Cov (x, y) = 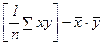5.

(доказательство эквивалентности указанных уравнений здесь опускается).

Дата добавления: 2014-01-20