Программа курса математики

Приклад 3.

Приклад 2.

Приклад 1.

Висновок.

Розв’язок неоднорідного рівняння при заданих крайових умовах подається формулою (**), де - функція Гріна для оператора.

Розв’язати рівняння:

ФСР:

Будуємо функцію Гріна:

- розв’зок.

Розв’язати рівняння:

Розв’язати рівняння:

література

Основна

1. Араманович И. Г., Левин В. И. Уравнения математической физики.
М.: Наука, 1969. 288 с.

2. Арсенин В. Я. Математическая физика. Основные уравнения и специальные функции. М.: Наука, 1966. 368 с.

3. Бицадзе А. В. Уравнения математической физики. М.: Наука,1976. 296 с.

4. Бицадзе А В. Некоторые классы уравнений в частных произ­водных. М.: Наука, 1981. 448 с.

5. Годунов С. К. Уравнения математической физики. М.: Наука,1979. 392 с.

6. Загускин В. Л. Справочник по численным методам решения уравнений.
М.: Наука, 1960. 200 с.

7. Кошляков С. Н., Глинер Э. Б., Смирнов М. М. Уравнения в частных производных математической физики. М.: Высш. шк., 1970. 710 с.

10.Курант Р. Уравнения с частными производными. М.: Мир, 1964, 830 с.

11.Михлин С. Г. Линейные уравнения в частных производных. М.: Высш. шк., 1977. 432 с.

12. Петровский И. Г. Лекции об уравнениях с частными производными. М.: Физматгиз, 1961. 300 с.

13. Положий Г. Н. Уравнения математической физики. М.:Высш. шк., 1964.

14. Смирнов В. И. Курс высшей математики: В 4 т. М.: Наука, 1981. Т. 1.-Т. 4.

15. Смирнов М. М. Задачи по уравнениям математической физики. М.: Наука, 1975. 128 с.

16. Соболев С. Л. Уравнения математической физики. М.:Наука, 1966. 444 с.

17. Стеклов Б. А. Основные задачи математической физики..: Наука, 1983. 432 с.

18. Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Наука, 1977. 724 с.

Додаткова література

19.Адамар Ж. Задача для линейных уравнений с частными производными гиперболического типа. М.: Наука, 1978. 352 с.

20.Бабаков И, И. Теория колебаний. М.: Наука, 1965. 200 с.

21. Окунєв Л. Я. Вища алгебра. К.: Наук, думка, 1950. 250 с.

22. Степанов В.В. Курс дифференциальных уравнений. М.:ГИФМЛ, 1958, 468с.

23. Фихтенгольц Г. М. Основы математического анализа: В 2 т.М.: Наука, 1968. Т. 2. 404 с.

(список основных вопросов к экзамену)

1 курс, 1 семестр, АВТФ (поток АВТ-1) 2012-2013 уч. г.

Модуль № 1 Дифференциальное исчисление функции одной переменной

§1. Функция одной переменной

1.1. Понятие функции. Переменная и область ее определения. Способы задания функций.

1.2. Понятие обратной функции.

1.3. Основные элементарные функции, их графики и свойства.

1.4. Суперпозиция функции (сложная функция, композиция функций, функция от функции)

§2. Предел последовательности

2.1. Последовательность как частный случай функции (функция целочисленного аргумента).

2.2. Предел последовательности и его геометрический смысл.

2.3. Теорема о пределе монотонной последовательности (формулировка)

§3. Предел функции в точке

3.1. Определение предела функции в точке и его геометрический смысл.

3.2. Бесконечно малые и бесконечно большие функции, сравнение бесконечно малых, эквивалентность бесконечно малых.

3.3. Основные свойства предельного перехода: переход к пределу в равенствах и неравенствах. Теорема об ограниченности функций, имеющих предел.

3.4. Первый и второй замечательный пределы (док-во для с/р из [1] том 1, глава 2, параграф 6,7).

3.5. Односторонние пределы (для с/р из [1] том 1, глава 2, параграф 2,3)..

§4. Непрерывность функции

4.1. Определение непрерывности функции в точке. Критерий непрерывности функции в точке.

4.2. Непрерывные элементарные и сложные функции.

4.3. Односторонняя непрерывность. Классификация разрывов функций.

4.4. Использование непрерывности функций для вычисления пределов. Предел сложной функций. Раскрытие неопределенностей в случае степенно-показательных выражений.

4.5. Свойства непрерывных функций на отрезке.

§5. Производная функции одной действительной переменной

5.1. Производная функции одной действительной переменной.

5.2. Геометрический и механический смысл производной, определение касательной и нормали к кривой.

5.3. Формула для приращения функции. Непрерывность функции, имеющей производную.

5.4. Простейшие правила вычисления производной.

5.5. Производная сложной функции, обратной, заданной неявно и параметрически (вывод для с/р из [1] том 1, глава 3, параграфы 9-18).

5.6. Понятие односторонней и бесконечной производных.

5.7. Производные основных элементарных функций (таблица производных; вывод для с/р из [1], том 1, глава 3, параграф 5 - 10).

5.8. Логарифмическая производная.

§6. Дифференциал функции

6.1. Определение дифференциала, его связь с производной.

6.2. Основные формулы и правила дифференцирования.

6.3. Инвариантность формы первого дифференциала. Применение дифференциала в приближенных вычислениях.

§7. Производные и дифференциалы высших порядков

7.1. Производные высших порядков для функций, заданных в явном виде.

7.2. Производные высших порядков для функций, заданных параметрически и неявным образом.

§8. Поведение функции на интервале (основные теоремы дифференциального исчисления; док-во для с/р из [1], том 1, глава 4, параграф 1 - 5).

8.1. Теорема Ферма.

8.2. Теорема Ролля.

8.3. Теорема Лагранжа (теорема о среднем).

8.4. Теорема Коши (обобщение теоремы Лагранжа).

8.5. Раскрытие неопределенностей. Правило Лопиталя.

§9. Исследование поведения функций

9.1. Условие монотонности функции.

9.2. Максимумы и минимумы. Необходимое и достаточное условие максимума и минимума. Общая схема нахождения экстремума.

9.3. Нахождение наименьшего и наибольшего значений функции на отрезке.

9.4. Выпуклость и вогнутость кривой, точки перегиба.

9.5. Асимптоты кривых (вертикальные, горизонтальные и наклонные).

9.6. Общая схема исследования функций и построения графиков.

Модуль № 2. Интегральное исчисление функции одной переменной
Глава 1. Неопределенный интеграл

§1. Неопределенный интеграл и простейшие приемы его вычисления

1.1. Понятие первообразной функции и неопределенного интеграла. Основные свойства и простейшие правила интегрирования.

1.2. Таблица основных интегралов.

1.3. Простейшие приемы интегрирования.

§2. Интегрирование путем замены переменной. Интегрирование по частям

2.1. Интегрирование путем замены переменной.

2.2. Интегрирование по частям.

2.3. Циклические интегралы. Рекуррентные формулы.

§3. Интегрирование рациональных выражений.

3.1. Интегрирование рациональных выражений.

3.2. Интегрирование простейших правильных дробей.

3.3. Разложение рациональных дробей на простейшие.

§4. Интегрирование иррациональных выражений.

4.1. Интегрирование иррациональных выражений вида: ;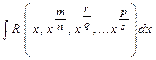

, где .

4.2. Подстановки Эйлера для интегралов вида: .

§5. Интегрирование тригонометрических функций.

5.1. Универсальная тригонометрическая подстановка. Интегрирование выражений вида: .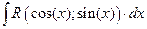

5.2. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок.

Глава 2. Определенный интеграл

§1. Постановка задачи. Нижние и верхние интегральные суммы.

1.1. Классы интегрируемых функций.

1.2. Основные свойства определенного интеграла. Определенный интеграл как функция верхнего предела.

1.3. Вычисление определенного интеграла. Формула Ньютона-Лейбница.

1.4. Замена переменной в определенном интеграле. Интегрирование по частям.

§2. Геометрическое и механическое приложения определенного интеграла

2.1. Вычисление площадей в прямоугольной декартовой системе координат.

2.2. Вычисление площади криволинейной трапеции для кривой, заданной параметрически.

2.3. Вычисление площадей в полярных координатах.

2.4. Вычисление длины дуги плоской кривой в прямоугольных декартовых координатах.

2.5. Вычисление длины дуги, заданной в параметрическом виде и в полярных координатах.

2.6. Вычисление объема тела вращения .

§3. Несобственные интегралы.

3.1. Интегралы с бесконечными пределами (несобственные интегралы первого рода).

3.2. Признаки сходимости несобственных интегралов первого рода. Абсолютная и условная сходимость.

3.3. Несобственные интегралы второго рода.

3.4. Признаки сходимости несобственных интегралов второго рода.

Дата добавления: 2014-01-20