Теоремы двойственности

Первая теорема двойственности. Для взаимодвойственных ЗЛП имеет место один из взаимоисключающих случаев;

1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают: max f () = min g ().

2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым,

4. Обе из рассматриваемых задач имеют пустые допустимые множества.

Экономический смысл первой теоремы двойственности. План производства X и набор оценок ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции с₁, с₂, …, c_n, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов у₁, у₂, …, y_m для всех же других планов и обеих задач прибыль от продукции всегда меньше (или равна) стоимости затраченных ресурсов: f() £ g(), т. е. ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Значит величина g() - f() характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных оценок ресурсов.

Из первой теоремы двойственности следует, что при оптимальных производственной программе и векторе оценок ресурсов производственные потери равны нулю.

Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану и получить максимальную прибыль либо продать ресурсы по оптимальным ценам и возместить от продажи равные ей минимальные затраты на ресурсы.

Вторая теорема двойственности (теорема о дополняющей нежесткости). Пусть X = (x₁,x₂,..., x_n) – допустимое решение прямой задачи (3.1)-(3.3), а = (y₁,у₂,..., y_т) - допустимое решение двойственной задачи (3.4)-(3.6). Для того чтобы они были оптимальными решениями соответствующих взаимодвойственных задач (3.1)-(3.3) и (3.4)-(3.6), необходимо и достаточно, чтобы выполнялись следующие соотношения:

	(4.7)
	(4.8)

Условия (4.7) и (4.8) позволяют, зная оптимальное решение одной из взаимодвойственных задач, найти оптимальное решение другой задачи.

Из второй теоремы двойственности в данном случае следуют такие требования на оптимальную производственную программу =(x ₁, x ₂,..., x_n) и оптимальный вектор оценок = (y₁, y₂, …, y_т):

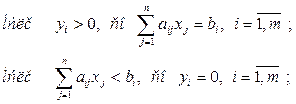
	(4.10)
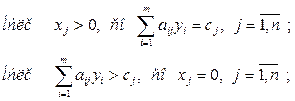
	(4.11)

Условия (4.10) можно интерпретировать так: если оценка y_i единицы ресурса i -гo вида положительна, то при оптимальной производственной программе этот ресурс используется полностью; если же ресурс используется не полностью, то его оценка равна нулю.

Из условия (3.11) следует, что если j -и вид продукции вошел в оптимальный план, то он в оптимальных оценках не убыточен; если же j -й вид продукции убыточен, то он не войдет в план, не будет выпускаться.

Рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Теорема об оценках. Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений – неравенств прямой задачи на величину D f ():

(4.9)

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи y_i в оптимальном плане называют, как выше уже отмечено, объективно обусловленными, или двойственными оценками.

Дата добавления: 2014-01-11