Определитель. Определение, свойства

Лекция 2

Рассмотрим числовую характеристику матрицы А, называемую определителем.

Обозначение определителя: det A, | A |,

det A =det=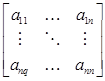

Положим

(*)

Здесь:

- суммирование ведется по всем возможным подстановкам n -ого порядка;

- сумма в правой части равенства (*) состоит из n! слагаемых, каждое из которых имеет вид 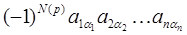(n! слагаемых, т.к. существует n! различных подстановок n -ого порядка);

- каждое такое произведение содержит ровно по одному элементу из каждой строки и каждого столбца матрицы А;

- знак каждого слагаемого в правой части равенства (*) зависит от четности соответствующей подстановки p.

Свойства определителей

Свойство 1. Определитель матрицы не меняется при её транспонировании:

det () =det A.

Свойство 2. Определитель матрицы, содержащий нулевую строку, равен нулю:

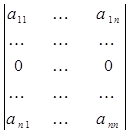=0.

Свойство 3. При перемене местами двух строк матрицы её определитель меняет знак:

=

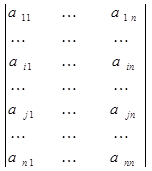Свойство 4. Определитель матрицы, имеющей две одинаковые строки, равен нулю.

Свойство 5. Общий множитель элементов некоторой строки определителя может быть вынесен за знак определителя:

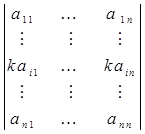= k

Свойство 6. Определитель матрицы, содержащей две пропорциональные строки, равен нулю.

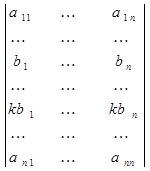=0.

Свойство 7.

i-тая строка =+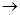

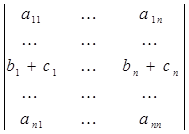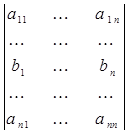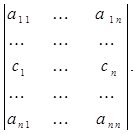
Свойство 8. Определитель матрицы не изменится, если к элементам одной из строк прибавить элементы другой строки, умноженные на некоторое число k:

=.

Определение. Строка вида называется линейной комбинацией строк .

Свойство 9. Если одна из строк матрицы является линейной комбинацией других её строк, то определитель такой матрицы равен нулю.

Замечание. Так как определитель матрицы не меняется при транспонировании, то сформулированные выше свойства справедливы и для столбцов.

Доказательства свойств 1 – 9.

Доказательство свойства 1.

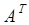Пусть А=; В==. Имеем: ,

Рассмотрим одно из слагаемых, входящих в определитель det В:

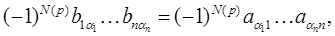
где p =

Произведение входит в качестве слагаемого в определитель det A со знаком, зависящим от четности подстановки :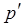

=

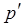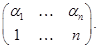
Четности подстановок 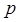и 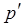совпадают, следовательно, определители матриц А и В состоят из одинаковых слагаемых, следовательно, det B =det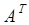=det A. ▲

Доказательство свойства 2.

Пусть матрица А содержит i – тую нулевую строку. Тогда каждое слагаемое, входящее в определитель det A, содержит в качестве множителя число 0 (как элемент i – той строки). Отсюда det A= 0. ▲

Доказательство свойства 3.

Пусть матрица В получена из матрицы В перестановкой i – той и j – той строк:

А =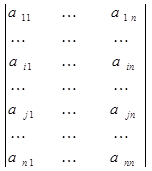; В =.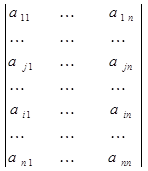

Рассмотрим одно из слагаемых, входящих в определитель det В:

=

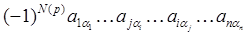
(здесь p =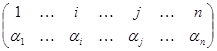). Произведение входит в определитель det B со знаком, определяемым четностью подстановки 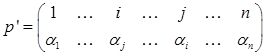. Подстановк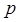и и 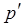отличаются одной транспозицией в нижней строке, следовательно, их четность различна. Следовательно, определители det A и det B состоят из одних и тех же слагаемых, но взятых с разными знаками. Отсюда det A = – det B. ▲

Доказательство свойства 4.

Пусть i – тая и j – тая строки матрицы А совпадают. Переставим эти строки. В силу свойства 3 определитель матрицы должен изменить знак. С другой стороны, матрица не изменилась, следовательно, её определитель не должен измениться: det A = – det A. Отсюда det A =0. ▲

Доказательство свойства 5.

Пусть i – тая строка матрицы А имеет вид (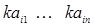). Имеем: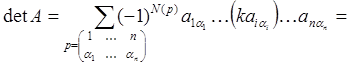

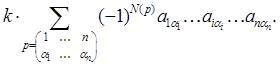
Следовательно, общий множитель элементов i – той строки может быть вынесен за знак определителя. ▲

Доказательство свойства 6.

Справедливость этого утверждения следует из справедливости утверждений в свойствах 5 и 6. ▲

Доказательство свойства 7.

Рассмотрим слагаемые, входящие в определитель в левой части равенства. Каждое такое слагаемое содержит в качестве множителя ровно один элемент i –той строки. Имеем:

=+

+.

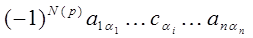Отсюда следует справедливость утверждения в свойстве 7. ▲

Доказательство свойств 8 – 9.

Справедливость утверждений в свойствах 8, 9 следует из утверждений в свойствах 6, 7. ▲

Примеры.

1. 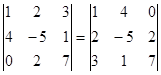(см. свойство 1);

2. (см. свойство 2);

3. (см. свойство 3);

4. 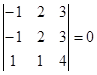(см. свойство 4);

5. 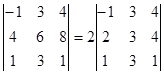(см. свойство 5);

6. , так как элементы второй строки в 2 раза больше соответствующих элементов первой строки (см. свойство 6);

7. 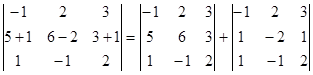(см. свойство 7);

8. 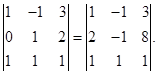Здесь определитель не изменился, когда к элементам второй строки прибавили соответствующие элементы первой строки, умноженные на 2 (см. свойство 8);

9. , т.к. элементы третьей строки являются суммами соответствующих элементов первой и второй строк (см. свойство 9).

Выведем общую формулу для вычисления определителя n -ого порядка. Используем равенство (*):

=+++++;

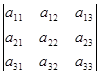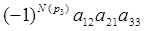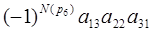Здесь - все возможные подстановки третьего порядка:

, , , ,,.

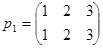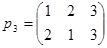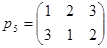Далее: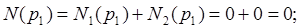

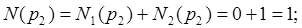
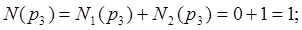
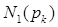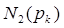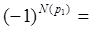
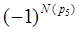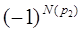(-число инверсий в верхней строке подстановки, - число инверсий в нижней строке подстановки). Имеем: - четные подстановки; -нечётные подстановки. Отсюда ==+1;

=== – 1.

Окончательно получаем общую формулу для определителя третьего порядка:

=--++-.

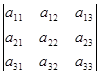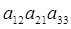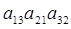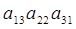Пример. Выясним, с каким знаком входит в определитель пятого порядка произведение .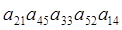

Составим соответствующую подстановку:

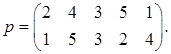
= N (2 4 3 5 1) =5 (т.к. инверсии образуют 5 пар элементов: (21), (43), (41), (31), (51)).

= N (1 5 3 2 4)=4 (т.к. инверсии образуют 4 пары элементов: (53), (52), (54), (32)).

Отсюда =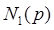+=5+4=9, p – нечетная подстановка, .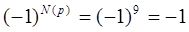

Вывод: это произведение входит в определитель пятого порядка со знаком

«–».

Дата добавления: 2014-01-20