Рассеяние частиц

15.1. Рассеяние частицы на силовом центре. Формула Резерфорда.

Рассмотрим снова рассеяние частицы на силовом центре.

Если на налетающую частицу действуют силы отталкивания, то, как мы установили в § 13, её движение всегда инфинитно, а траектория частицы - гипербола.

Для рассмотрения задачи введем

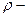прицельное расстояние – длина

перпендикуляра, опущенного из

рассеивающего центра на направление

касательной к траектории (асимптоту гиперболы)

находящейся на бесконечно большом удалении

от центра частицы,

угол рассеяния частицы,

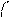
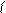
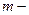масса частицы,

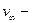скорость налетающей частицы на

бесконечно большом удалении от центра.

Угол определяет наклон асимптот гиперболы, по которой движется рассеиваемая частица (см. рисунок и уравнение (13.17)), к оси и связан с углом рассеяния очевидным соотношением

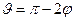(15.1)

Значение угла может быть найдено из уравнения (13.17), если положить, что частица находится на бесконечно большом удалении от рассеивающего центра (). В этом случае уравнение (13.17) приводится к виду:

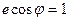и 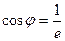. (15.1а)

Тогда, с учетом (15.1) и (15.1а),

.

Учитывая (13.5), получаем

. (15.2)

На бесконечно большом расстоянии от рассеивающего центра (, ), полная энергия и момент импульса частицы равны

. (15.3)

Подставляя эти величины в выражение (15.2), получаем формулу, связывающую угол рассеяния с прицельным параметром :

. (15.4)

Заметим, что при движении частицы в поле притяжения () связь между углом рассеяния и прицельным параметром получается точно такой же, т.е. также выражается формулой (15.4).

Задача о рассеянии на силовом центре имеет важное практическое значение. Однако, формулу (15.4) не удается непосредственно использовать для описания результатов эксперимента, т.к. она написана для определенного прицельного параметра и определяет индивидуальное отклонение частицы. В эксперименте же мы имеем дело не с отдельной частицей, а наблюдаем рассеяние целого пучка одинаковых частиц, падающих на рассеивающий центр с одинаковыми скоростями 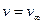, но с разными значениями прицельного параметра . Следовательно, и рассеиваются частицы под разными углами .

Поэтому в физике вводится другая, очень важная, характеристика процесса рассеяния - сечение или эффективное сечение.

15.2. Эффективное сечение рассеяния.

Определение: Эффективное сечение рассеяния - величина, характеризующая вероятность перехода системы сталкивающихся частиц в результате их рассеяния (как упругого, так и неупругого) в определенное конечное состояние.

Конечное состояние каждой частицы пучка характеризуется углом , под которым она рассеялась. Обозначим через 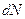число частиц, рассеиваемых в единицу времени на углы, лежащие в интервале от до .

Само значение 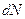зависит от числа падающих

Пучок        

частиц, точнее от плотности частиц в потоке, и

поэтому его неудобно использовать для

характеристики процесса рассеяния.

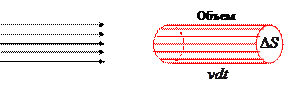
Пусть плотность падающих частиц, а

их скорость в направлении движения пучка.

Тогда число падающих на поперечную площадку 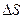частиц за время равно

,

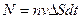т.е. числу частиц, находящихся в объеме

.

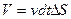Значит, за единицу времени через единицу площади площадки 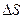проходит

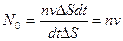частиц,

где плотность потока частиц.

В этом случае эффективное сечение рассеяния определяется как

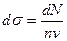(15.5)

Размерность сечения равна размерности площади, т.к. , , , откуда получаем .

Величина эффективного сечения (15.5) полностью определяется видом рассеивающего поля и является важнейшей характеристикой процесса рассеяния. Эта характеристика измеряется экспериментально и служит для определения структуры сталкивающихся частиц.

Если связь между переменными и взаимно

однозначна, как это имеет место в классической

механике, то под углами, лежащими от до

, рассеиваются только те частицы, которые

летят в некотором интервале значений прицельного

расстояния от до (угол рассеяния

монотонно убывает с ростом прицельного расстояния).

Тогда число частиц, рассеивающихся в единицу

времени в интервал углов (), равно

. (15.6)

Т.о., сечение рассеяния может быть выражено через

прицельное расстояние как

. (15.7)

Часто бывает удобно характеризовать сечение углами,

под которыми вылетают частицы:

. (15.8)

Частицы, испытавшие рассеяние на силовом центре, продолжают свое движение, распределяясь в некоторой

области пространства. Поэтому для описания задачи наряду с плоскими вводят телесные (пространственные)

углы.

Элементарный телесный угол определяется как

, (15.9)

где элемент поверхности сферы радиуса .

Любая поверхность , опирающаяся на элемент

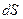, характеризуется тем же телесным углом .

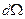Любой замкнутой сферической поверхности, от центра которой ведется отсчет, соответствует телесный угол, равный

. (15.10)

Т.о., полный телесный угол равен .

В задачах рассеяния телесный угол, вырезающий область пространства, в пределах которого разлетаются частицы в результате взаимодействия с силовым центром, имеет форму раструба – конусный угол.

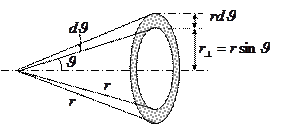Найдем связь между телесным углом 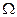, характеризующим результат рассеяния и параметрами столкновения и .

Площадь элемента сферической поверхности,

вырезаемый конусами, задаваемыми углами

и , равна

поэтому

. (15.11)

Тогда сечение рассеяния (дифференциальное сечение):

. (15.12)

Зная зависимость , получим сечение рассеяния как функцию угла . Чтобы найти полное сечение рассеяния 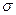, надо проинтегрировать (15.12) по всем углам.

15.3. Упругое рассеяние на твердом шаре.

Найдем полное сечение рассеяния на твердом шаре радиусом 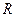, используя выражение (15.8).

Воспользовавшись рисунком, получаем связь между параметрами и :

.

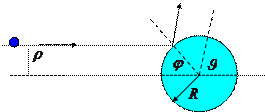
Теперь вычисляем производную:

и, подставляя в выражение (15.8), получаем

дифференциальное сечение рассеяния:

,

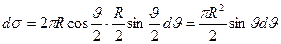или через телесный угол с вершиной в центре шара:

. (15.13)

Из (15.13) следует, что рассеяние в 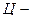системе изотропно.

Полное сечение рассеяния на твердом шаре равно

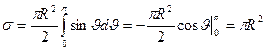. (15.14)

Т.о., прицельная площадь, куда должна попасть частица, чтобы рассеяться, равна площади сечения шара.

15.4. Кулоновское рассеяние.

Рассеяние заряженных частиц на кулоновском центре описывается формулой Резерфорда. Получим эту формулу, принимая в расчет, что связь между параметрами столкновения (, и ) дается формулой (15.4). Используя (15.4), запишем квадрат прицельного параметра, продифференцируем полученное выражение и подставим результат в формулу (15.7), выражающую сечение рассеяния через прицельное расстояние:

,

.

Для эффективного сечения имеем (15.7)

.

И окончательно для эффективного сечения рассеяния получаем выражение вида:

. (15.15)

Для рассеяния частиц на ядрах элементов с порядковым номером 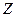, подставляя в (15.15) , приходим к знаменитой формуле Резерфорда:

. (15.16)

Для сравнения расчетного значения с экспериментом необходимо еще просуммировать по числу ядер 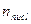в единице объема (1 см³) образца (фольги), и, если ядра не перекрывают друг друга, то измеряемое сечение будет равно

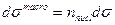(15.17)

В эксперименте Резерфордом проверялась следующая величина:

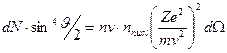. (15.18)

Условия эксперимента не менялись, поэтому правая часть уравнения (15.18) остается постоянной и число рассеянных под углом частиц должно быть пропорционально .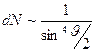

Т.о., путем сравнения результатов, полученных в опытах Резерфорда, и их сравнением с формулой Резерфорда удалось установить, что частицы рассеивает точечный центр с положительным зарядом ядро.

Дата добавления: 2014-01-20