Основные параметры лопаточных машин и кинематика потока в решетках

Лопаточные решетки (лопаточные венцы), образующие ступень лопаточной машины, трехмерны. Лопатки обтекаются пространственным неустановившимся потоком жидкости ограничиваются рассмотре­нием установившегося обтекания плоских решеток двухмерным потоком по ряду сечений, т. е. рассматривают идеализированные схемы течения с цилиндрическими поверхностями тока для осевых машин и плоскими поверхностями тока для чисто радиальных машин.

Рассмотрим сначала единичный лопаточный профиль.

Средняя линия профиля- геометрическое место центров окружностей, вписанных в профиль. Хорда профиля- линия, соединяющая наиболее удаленные точки средней линии профиля. Корыто- вогнутая часть профиля. Спинка- выпуклая часть профиля. - максимальная часть профиля или максимальный диаметр окружности, вписанной в профиль. - максимальный прогиб средней линии профиля или наибольшее удаление средней линии профиля от хорды.

В общем случае любая точка профиля может быть задана двумя координатами х и у. Координаты точек, образующих спинку, имеют индекс «с», а координаты точек, обра­зующих корыто, - индекс «к».

Часто величины, характеризующие профиль, задаются в относительных координатах, в долях от хорды . Например, , , 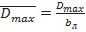и т.д.

Плоская прямая лопаточная решетка. Получается при развертке сечения лопаток осевой машины цилиндрической поверхностью с осью, совпадающей с осью вращения.

Линия 1-1 (см. рис. 2.8), проходящая через крайние -точки кро­мок профилей, называется входным фронтом плоской решетки. Линия 2-2, проходящая через крайние точки выходных кромок профилей, образует выходной фронт решетки. В плоской прямой решетке фронтом является прямая линия.

Расстояние по фронту между соответствующими точками сосед­них профилей называется шагом решетки t. Для прямой решетки шаг на входе в решетку равен шагу на выходе из нее. Угол между хордой профиля и фронтом плоской решетки называется установочным углом (см. рис. 2.8). Ши­рина решетки b - расстояние по нормали между фронтами решетки.

Обычно входной угол профиля в решетке определяется как угол между касательной к средней линии профиля в начальной ее точке и входным фронтом решетки или касательной к входному фронту решетки (см. рис. 2.8). Аналогично определяется выходной угол лопатки .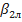

Угол 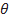характеризует угол изгиба лопатки 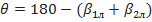, град.

Важным параметром плоских решеток является густота .

Плоская круговая лопаточная решетка. Получается при сечении лопаток радиальной машины плоскостью, перпендикулярной оси вращения.

В плоской круговой решетке фронтом является окружность. Шаг решетки на входе и на выходе отличаются друг от друга.

; ,

где 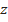- количество лопаток.

определяется как угол межу касательной к средней линии профиля в начальной ее точке и касательной к входному фронту решетки, аналогично и .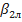

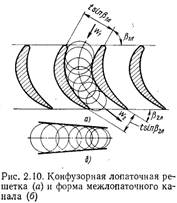
Форма межлопаточного канала. О форме межлопаточного канала решетки можно судить, если между соседними профилями вписать окружности так, чтобы они касались обоих профилей (рис. 2.10). Центры этих окруж­ностей образуют среднюю линию межлопаточного канала.

1) В конфузорной лопаточной решетке межлопаточный канал сужается, обеспечивая ускорение дозвукового потока.

2) В диффузорной лопаточной решетке межлопаточный канал расширяется, обеспечивая торможение дозвукового потока.

3) Решетка имеет одинаковые проходные сечения и на входе и на выходе- такие решетки применяются в активных лопаточных машинах.

Турбинные решетки, как правило, конфузорные, решетки компрессоров и насосов- диффузорные. Активные решетки применяются и в тех и в других машинах.

Кинематические соотношения в лопаточных машинах

В общем случае вектор абсолютной скорости можно разложить на три составляющих: окружную , радиальную и осевую (рис. 2.13) (в дальнейшем для упрощения за­писи знак вектора над символом, обозначающим скорость, будем да­вать, только когда векторную вели­чину можно принять за скалярную). Окружная составляющая скорости лежит в плоскости вращения и на­правлена по линии вектора окружной скорости. Радиальная и осевая составляющие лежат в плоскости, которая называется мериди­ональной. Эта плоскость проходит через ось вращения лопаточной машины. Проекции скоростей на эту плоскость будем обозначать индексом m.

Меридиональная составляющая скорости 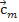является суммой радиальной и осевой составляющих (см. рис. 2.13):

Абсолютная скорость полностью определяется меридиональной составляющей 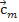и окружной составляющей скорости :

Окружная составляющая характеризует «закрутку» потока и непосредственно связана с удельной работой. Меридиональная составляющая определяется объемным расходом жидкости через лопаточную машину и площадью нормаль­ного к направлению составляющей 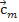сечения, которую будем обо­значать F_m. В общем случае , где - коэффициент сужения сечения потока (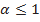); - площадь расчетного проходного сечения.

Обычно полагаем . Скорость 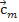находится из уравнения неразрывности

, (7.1)

где - массовый расход, кг/с; - плотность, кг/м³. Для = const

, (7.2)

где - объемный расход, м³/с.

Зная абсолютную скорость жидкости с и окружную скорость колеса (переносную скорость) u, легко найти, применяя общее правило сложения скоростей сложного движения, скорость жидко­сти относительно перемещающейся лопатки — относительную ско­рость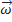

(7.3)

Эти три вектора лежат в одной плоскости, заштрихованной на рис. 2.13. Перенося эту плоскость на плоскость чертежа, можем получить для любой лопаточной машины план скоростей, или треугольник скоростей, т. е. векторную связь абсолютной, относитель­ной и окружной скоростей. Для чисто осевой лопаточной машины меридиональная составляющая скорости равна осевой, а для чисто радиальной машины она равна радиальной составляющей скорости, т. е. для осевой машины = 0 и = , а для радиальной = 0 и = .

Следовательно, для осевой лопаточной машины параллелепипед, получаемый при разложении вектора абсолютной скорости на со­ставляющие (см. рис. 2.13), заменится параллелограммом, располо­женным в плоскости, касательной к цилиндрической поверхности (рис. 2.14). В этой плоскости и будет производиться построение пла­нов скоростей для осевой машины.

Для чисто радиальной лопаточной машины параллелепипед вектора абсолютной скорости заменяется параллелограммом, в пло­скости которого, являющейся плоскостью вращения, и будет произ­водиться построение планов скоростей (рис. 2.15).

Вход в колесо

Предолоим, что вектор аб­солютной скорости на входе в меж­лопаточные каналы известен или его можно найти. В общем случае он определяется двумя составля­ющими - меридиональной и окружной . Меридиональная составляющая определяется объемным расходом и площадью нормального к этой составляющей проходного сечения колеса непосредственно перед лопатками см. уравнение (7.2).

Окружная составляющая скорости на входе находится из условий течения жидкости в подводящем устройстве.

Для входа в колесо можно записать соотношение

, (7.4)

где — окружная скорость средней точки входных кромок ло­паток.

Скорости , и лежат в плоскости, проходящей через век­торы и . При построении планов эту плоскость совмещают с плоскостью чертежа. Примем направление вертикали в плоскости чертежа за меридиональное направление (направление скорости ), тогда окружная скорость их изобразится отрезком горизонтальной линии и найдется как разность векторов и (рис. 2.16).

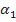- это угол между направлением потока в абсолютном движе­нии и направлением окружной скорости, - это угол между на­правлением, потока в относительном движении, определяемым век­тором и направлением окружной скорости для турбины и обрат­ным направлением для насоса. В общем случае угол 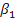может не совпадать с входным углом лопатки , т. е. поток может натекать с углом атаки. Угол атаки i определяется углом между вектором скоро­сти и касательной к средней линии профиля лопатки на входе. Участок касательной на рис. 2.16 отштрихован.

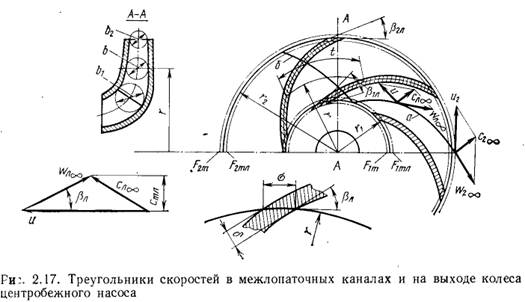
Течение по межлопаточным каналам колеса и на выходе из колеса

Для того чтобы найти абсолютную скорость жидкости в любой точке межлопаточного канала на некотором расстоянии от входа на лопатки, надо произвести векторное сложение относи­тельной скорости жидкости в канале 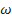и переносной скорости u. Относительная скорость 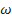внутри межлопаточного канала найдется по направлению, которое определяется в первом приближении направлением средней линии лопатки (углом 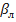), и меридиональной составляющей скорости с учетом толщины лопаток (рис. 2.17).

Предположение относительно того, что направление касательной к средней линии профиля параллельно вектору относительной ско­рости, строго говоря, справедливо лишь для решетки, состоящей из бесконечно большого числа бесконечно тонких профилей. При необходимости векторы скоростей, соответствующие этой расчетной схеме, будем отмечать знаком , так как полагаем, что число лопа­ток .

Для нахождения осредненной скорости внутри межлопаточного канала необходимо учитывать толщину профиля вместе с толщиной вытеснения пограничного слоя. При отрывном обтекании следует учитывать толщину отрывной зоны. В первом приближении учиты­вается только толщина лопаток (например, в насосах).

Определение меридиональной скорости с учетом толщины лопаток для точки, расположенной на произвольном радиусе r, проведем на примере центробежного колеса (см. рис. 2.17, индексы 1 и 2 здесь и далее соответствуют входу в колесо и выходу из него). Площадь проходного сечения колеса обозначим , площадь проходного сече­ния на том же радиусе с учетом толщины лопаток обозначим 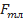. Отношение представляет собой коэффициент сужения сечения колеса. Обозначим его k. Площади и 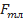можно вычислить через шаг лопаток

,

где z — число лопаток.

Тогда

, (7.5)

(7.6)

Здесь - толщина лопаток, определенная по дуге окружности; - ширина меридионального сечения колеса. Связь между нормальной толщиной 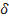и толщиной легко устанавливается при рас­смотрении рис. 2.17:

. (7.7)

Для нахождения меридиональной скорости с учетом толщины лопаток воспользуемся формулой, непосредственно вытекающей из уравнения (7.2):

Здесь - меридиональная скорость с учетом толщины лопаток, -меридиональная скорость без учета толщины лопаток. С учетом выражений (7.3) и (7.4) можно записать

. (7.8)

Относительная скорость в произвольном сечении колеса с учетом толщины лопаток найдется построением треугольника скоростей по известным скоростям и u и по углу 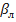(см. рис. 2.17) или из соот­ношения

. (7.9)

Треугольники скоростей на выходе из колеса строятся так же, как и для произвольного сечения, но без учета сужения сечения лопатками.

На рис. 2.17 показано взаимное расположение векторов ско­ростей относительного 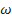, переносного u и абсолютного движения с на примере центробежной лопаточной машины (насоса) для произ­вольного и выходного радиусов. Там же показаны линии тока жидко­сти для колеса центробежного насоса (при ) в относительном и абсолютном движении.

Дата добавления: 2014-01-20