
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основное уравнение лопаточных машин
|
|
|
|
Между потоком жидкости и лопатками рабочего колеса осуществляется силовое взаимодействие. Это взаимодействие создает разность давлений жидкости на лопатках вращающегося колеса, что позволяет передать энергию от колеса к жидкости и наоборот. У насоса (компрессора) эта разность давлений определяет основную часть момента сопротивления на валу, у турбины - крутящего момента.
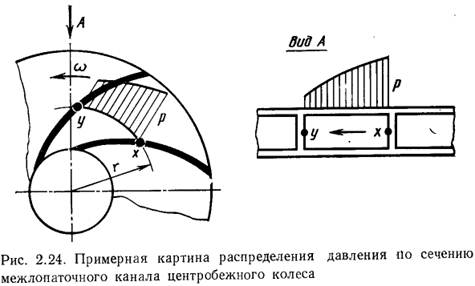 На рис. 2.24 для примера приведено распределение давления по сечению межлопаточного канала колеса центробежного насоса. Вследствие неравномерности распределения давления и скорости при установившемся характере относительного движения жидкости через рабочее колесо абсолютное движение жидкости через колесо будет иметь неустановившийся характер (Если бы распределение давления было равномерным, то на валу возникал бы момент. Таким образом, нестационарность абсолютного движения необходима для передачи энергии). В самом деле, каждая частица колеса периодически проходит мимо корпуса. Мгновенная абсолютная скорость в любой точке будет циклически изменяться в соответствии с изменением относительной скорости в межлопаточном канале. Следовательно, в абсолютном движении не будет выдерживаться характерный признак установившегося движения - постоянство скорости в данной точке пространства. Но, рассматривая осредненные по сечению канала значения скоростей, можно применять основные законы механики для установившегося движения к абсолютному движению жидкости в колесе.
На рис. 2.24 для примера приведено распределение давления по сечению межлопаточного канала колеса центробежного насоса. Вследствие неравномерности распределения давления и скорости при установившемся характере относительного движения жидкости через рабочее колесо абсолютное движение жидкости через колесо будет иметь неустановившийся характер (Если бы распределение давления было равномерным, то на валу возникал бы момент. Таким образом, нестационарность абсолютного движения необходима для передачи энергии). В самом деле, каждая частица колеса периодически проходит мимо корпуса. Мгновенная абсолютная скорость в любой точке будет циклически изменяться в соответствии с изменением относительной скорости в межлопаточном канале. Следовательно, в абсолютном движении не будет выдерживаться характерный признак установившегося движения - постоянство скорости в данной точке пространства. Но, рассматривая осредненные по сечению канала значения скоростей, можно применять основные законы механики для установившегося движения к абсолютному движению жидкости в колесе.
Для определения суммарного момента, действующего на колесо при движении через него жидкости, применим теорему о моменте количества движения: момент равнодействующей внешних сил, приложенных к выделенному объему, равняется изменению момента количества движения массы жидкости, протекающей в единицу времени через этот объем.
Возьмем объем V, ограниченный поверхностями 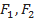 и
и  т. е. включающий в себя все каналы (рис. 2.25).
т. е. включающий в себя все каналы (рис. 2.25).
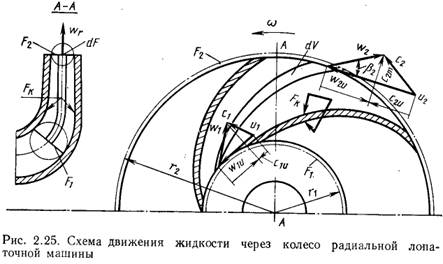
Изменение момента количества движения в окружном направлении
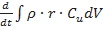
равно суммарному моменту Мж внешних сил относительно оси вращения. Следовательно, в общем случае для неустановившегося режима
 (7.10)
(7.10)
Полную производную в правой части уравнения (7.1) можно представить как сумму локальной производной, которая учитывает изменение за время dt момента количества движения в рассматриваемом объеме в связи с неустановившимся характером движения, и конвективной производной, определяющей изменение момента количества движения за то же время из-за перехода рассматриваемого объема жидкости в другое положение:
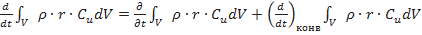 (7.11)
(7.11)
Конвективная производная по времени от интеграла некоторой величины, взятого по движущемуся объему, равна переносу той же величины сквозь контрольную поверхность, ограничивающую этот объем. Перенос количества движения происходит только через поверхности 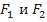 поэтому из формул (7.1) и (7.2) получим
поэтому из формул (7.1) и (7.2) получим
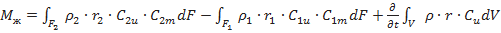 (7.12)
(7.12)
Уравнение (7.3) определяет момент, приложенный к жидкости, в общем случае (в том числе на неустановившемся режиме). Первые два члена уравнения (7.13) характеризуют момент, приложенный к жидкости, на установившемся режиме. Следовательно, на установившемся режиме
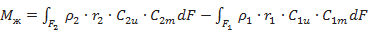 (7.14)
(7.14)
Выражая массовый расход как
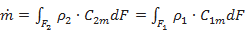 (7.15)
(7.15)
и понимая под  и
и  скорости, осредненные по поверхностям
скорости, осредненные по поверхностям  и
и 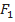 (
(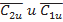 ), соотношение (7.4) получим в виде
), соотношение (7.4) получим в виде
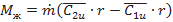 (7.16)
(7.16)
Суммарный момент внешних сил 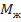 складывается из момента
складывается из момента 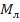 от воздействия колеса (поверхности
от воздействия колеса (поверхности  на рис. 2.25) на жидкость в выделенном объеме и моментов
на рис. 2.25) на жидкость в выделенном объеме и моментов 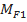 и
и 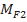 поверхностных сил, действующих по граничным поверхностям
поверхностных сил, действующих по граничным поверхностям 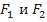 . Из объемных сил только силы тяжести будут внешними, но вследствие осевой симметрии они дают относительно оси колеса момент, равный нулю. Из поверхностных сил, действующих на граничных поверхностях, моменты
. Из объемных сил только силы тяжести будут внешними, но вследствие осевой симметрии они дают относительно оси колеса момент, равный нулю. Из поверхностных сил, действующих на граничных поверхностях, моменты 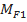 и
и 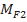 относительно оси вращения могут давать только касательные напряжения, т. е. силы трения, обусловливаемые турбулентным обменом импульсами. Силы давления на граничных поверхностях, как нормальные, не дают момента относительно оси:
относительно оси вращения могут давать только касательные напряжения, т. е. силы трения, обусловливаемые турбулентным обменом импульсами. Силы давления на граничных поверхностях, как нормальные, не дают момента относительно оси:
 (7.17)
(7.17)
Уравнение (7.6) показывает, что изменение момента количества движения жидкости в абсолютном движении через колесо насоса равно суммарному моменту сил, действующих на выделенный объем. Пренебрегая моментами поверхностных сил, действующих на поверхности 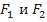 ограничивающие колесо лопаточной машины, и на внутренние поверхности, ограничивающие лопатки по ширине, получим момент в ньютонах на метр, действующий со стороны лопаток на жидкость,
ограничивающие колесо лопаточной машины, и на внутренние поверхности, ограничивающие лопатки по ширине, получим момент в ньютонах на метр, действующий со стороны лопаток на жидкость,
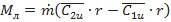 (7.18)
(7.18)
Зная момент 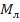 , можно определить мощность в ваттах как произведение момента в ньютонах на метр на угловую скорость вращения в радианах на секунду. Назовем ее окружной мощностью (словом «окружная» подчеркивается, что речь идет о лопаточной решетке, а не о машине в целом). Окружная мощность Nu определяется уравнением
, можно определить мощность в ваттах как произведение момента в ньютонах на метр на угловую скорость вращения в радианах на секунду. Назовем ее окружной мощностью (словом «окружная» подчеркивается, что речь идет о лопаточной решетке, а не о машине в целом). Окружная мощность Nu определяется уравнением
 (7.19)
(7.19)
Отнеся мощность (в ваттах) к массовому секундному расходу в килограммах на секунду, получим выражение для удельной работы лопаточной машины в джоулях на килограмм. Удельная работа - это энергия, переданная колесом единице массы жидкости,
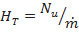 (7.20)
(7.20)
Если выразить  через момент
через момент 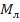 , то получим
, то получим
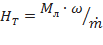 (7.21)
(7.21)
Применительно к насосу эту величину будем называть теоретическим напором и обозначать  .
.
Подставляя развернутое выражение для Мл в уравнение (7.8), получим
 (7.22)
(7.22)
где  - теоретический напор, Дж/кг (м2/с2).
- теоретический напор, Дж/кг (м2/с2).
Записанное в этом виде уравнение носит название уравнения Эйлера для лопаточных машин-исполнителей (насосов). Оно справедливо и для лопаточных машин-двигателей (турбин). Момент от воздействия потока на колесо
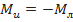 (7.23)
(7.23)
Соответственно для лопаточной машины-двигателя
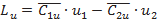 (7.24)
(7.24)
где  —удельная работа, Дж/кг (м2/с2).
—удельная работа, Дж/кг (м2/с2).
Для осевых лопаточных машин 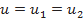 и уравнения Эйлера для машин-исполнителей и машин-двигателей запишутся в наиболее простом виде
и уравнения Эйлера для машин-исполнителей и машин-двигателей запишутся в наиболее простом виде
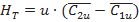 (7.25)
(7.25)
 (7.26)
(7.26)
Анализ уравнений Эйлера показывает следующее:
1. Удельная работа лопаточной машины, выраженная в джоулях на килограмм, не зависит от рода рабочего тела, так как его физические параметры не входят в уравнение Эйлера. Эта работа зависит только от окружных составляющих абсолютных скоростей и окружных скоростей вращения колеса.
2. Жидкость передает энергию колесу, когда 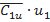 >
> 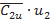 и наоборот, колесо передает энергию жидкости, когда
и наоборот, колесо передает энергию жидкости, когда 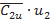 >
>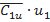 . Лопаточные машины, передающие энергию от жидкости к колесу, являются машинами-двигателями (турбинами), а передающие внешнюю механическую энергию газу или жидкости, являются машинами-исполнителями (компрессорами или насосами).
. Лопаточные машины, передающие энергию от жидкости к колесу, являются машинами-двигателями (турбинами), а передающие внешнюю механическую энергию газу или жидкости, являются машинами-исполнителями (компрессорами или насосами).
3. Удельная работа лопаточной машины будет тем больше, чем больше окружная составляющая абсолютной скорости  и окружная скорость u, входящие в первые члены уравнений (7.12) и (7.14). Для турбины это означает необходимость обеспечения сопловым аппаратом такого направления скорости
и окружная скорость u, входящие в первые члены уравнений (7.12) и (7.14). Для турбины это означает необходимость обеспечения сопловым аппаратом такого направления скорости  , чтобы окружная составляющая
, чтобы окружная составляющая  имела большое значение. Для насоса (компрессора) необходимое значение
имела большое значение. Для насоса (компрессора) необходимое значение  обеспечивается отклонением потока в рабочем колесе, т. е. углом лопаток колеса на выходе
обеспечивается отклонением потока в рабочем колесе, т. е. углом лопаток колеса на выходе 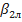 : чем больше
: чем больше 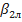 тем больше будет
тем больше будет  . Большая окружная скорость
. Большая окружная скорость  для турбины и
для турбины и 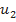 для насоса может быть получена при большой частоте вращения (
для насоса может быть получена при большой частоте вращения (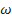 или при больших радиусах колеса
или при больших радиусах колеса 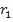 для турбины и
для турбины и 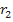 для насоса).
для насоса).
4. Удельная работа лопаточной машины на окружности колеса будет больше, если окружные составляющие скорости, которые входят во вторые члены уравнений (7.12) и (7.14), будут иметь иной знак, чем окружные составляющие скорости в первых членах этих уравнений.
Для насоса и компрессора это означает, что при закрутке потока на входе в сторону, обратную вращению, напор машины будет увеличиваться, а при закрутке потока в сторону вращения - снижаться.
Для турбины закрутка потока на выходе из колеса в сторону вращения уменьшает работу турбины. Наличие окружной составляющей скорости на выходе из турбины, направленной в сторону, обратную вращению, увеличивает работу турбины, однако снижает ее экономичность.
Уравнение энергии относительного движения (вывод уравнения Эйлера)
Данное уравнение связывает поля скоростей и давлений. В абсолютном установившемся движении несжимаемой жидкости без обмена энергии с внешней средой уравнение энергии известно в форме уравнения Бернулли
 .
.
Абсолютное движение потока во вращающемся колесе является неустановившимся, поэтому необходимо рассматривать уравнение энергии при установившемся относительном движении потока в колесе. Уравнение движения жидкости в направлении перемещения
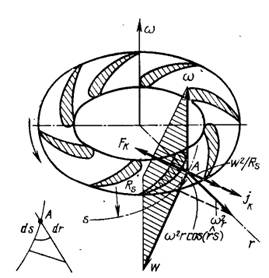
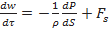 , м/с2,
, м/с2,
где  - элемент линии тока;
- элемент линии тока;  - проекция массовых сил на напрвление перемещения, отнесенная к единице массы.
- проекция массовых сил на напрвление перемещения, отнесенная к единице массы.
При относительном движении к массовым силам относятся центробежные силы инерции 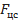 , напрвленные по радиусу, и кориолисовы силы
, напрвленные по радиусу, и кориолисовы силы 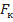 , направленные перепендикулярно направлению перемещения
, направленные перепендикулярно направлению перемещения
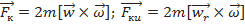 .
.
Влиянием силы тяжести и ускорением ракеты на течение в центробежном колесе пренебрегаем. Проекция кориолисовой силы в направлении перемещения равна нулю т. к. она перпендикулярна. Проекция центробежной силы на направление перемещения равна
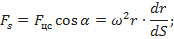
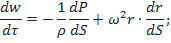
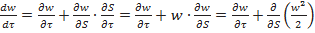 .
.
При установившемся относительном движении  .
.
 ;
;
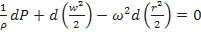 .
.
Интегрируя уравнение для расчетных сечений 1-1 и 2-2, получим для несжимаемой жидкости
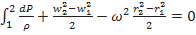 ;
;
 ;
;
 .
.
Если учесть, что изменение удельной работы  , а
, а 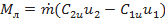 и
и  , можно получить уравнение Эйлера в первой форме для турбины и насоса
, можно получить уравнение Эйлера в первой форме для турбины и насоса
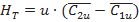
 .
.
Рассмотрим вторую форму уравнений Эйлера
Из треугольника скоростей, воспользовавшись теоремой косинусов запишем
 ; (7.27)
; (7.27)
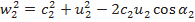 .
.
При этом 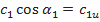 , a
, a 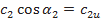 .
.
Поэтому выражения (7.27) приобретают вид
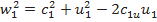 ;
;
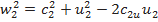 .
.
Или 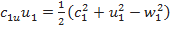 ;
;
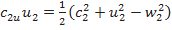 .
.
Удельная теоретическая работа насоса (компрессора)
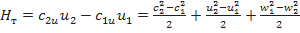 . (*)
. (*)
Удельная теоретическая работа турбины
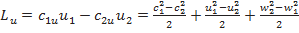 . (**)
. (**)
Для осевой турбины 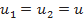
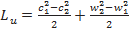 .
.
Выявим физический смысл каждого члена. Приращение кинетической энергии жидкости в абсолютном движении составит динамический напор колеса
 .
.
Очевидно, что оставшиеся члены в уравнении (*) составит приращение потенциальной энергии. Будем называть эту величину статическим напором колеса
 ;
;
член 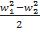 представляет собой изменение кинетической энергии в относительном движении и показывает, что для увеличения давления необходимо тормозить поток в относительном движении.
представляет собой изменение кинетической энергии в относительном движении и показывает, что для увеличения давления необходимо тормозить поток в относительном движении.
Член 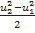 в уравнении (*) представляет собой работу центробежных сил для массы равной 1 килограмм.
в уравнении (*) представляет собой работу центробежных сил для массы равной 1 килограмм.
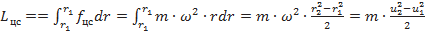 ;
;
Аналогично действуем и для уравнения (**).
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2536; Нарушение авторских прав?; Мы поможем в написании вашей работы!