Решение уравнений первого порядка

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Практикум

Given

Решение задач оптимизации в приложениях Mathcad и Excel

В приложении Mathcad имеются встроенные функции, с помощью которых можно решать задачи оптимизации. Рассмотрим пример.

Пусть требуется определить оптимальные значения x ₁ и x ₂, которые обеспечивали бы максимум целевой функции

y=1,7+4,56x₁-3x₂-0,69x₁x₂-0,44x₂²

и удовлетворяли ограничениям:

3 <=x₁<=4, 0,1<=x₂<=0,9

В рабочей области приложения Mathcad требуется записать:

f(x1, x2):= 1,7+4,56x1-3x2-0,69x1x2-0,44x2²

x1:= 3

x2:=0.1

4≥ x1 ≥ 3

0.9 ≥ x2 ≥ 0.1

R:= maximize(f, x1, x2)

R =

Встроенная функция minimize позволяет решить задачи оптимизации, в которых нужно определить минимум целевой функции.

В приложении Excel имеется специальная команда, с помощью которой можно решать задачи оптимизации. Например, чтобы решить предыдущий пример, можно произвести следующие действия.

– на рабочем листе, например в ячейке А1 записать значение левой границы для первого ограничения (число 3);

– в ячейке В1 записать значение левой границы для второго ограничения (число 0,);

– в ячейке С1 записать целевую функцию:

=1,7+4,56∙А1-3∙В1-0,69∙А1∙В1-0,44∙В1^2

– выполнить Сервис/Поиск решения. В появившемся окне задать имя ячейки с целевой функцией (для данного примера С1), определить, что в задаче целевая функция стремится к максимуму, ввести соответствующие ограничения для содержимого ячеек А1 и В1.

Решение задачи можно посмотреть и проанализировать на отдельном листе.

Рисунок и пр.

Если в пункте меню Сервис команда Поиск решения отсутствует, то её можно добавить, используя Сервис/Настройка.

В табл.26.1 приведены данные для оптимизации процессов, модели которых в виде уравнений регрессии приведены в табл. 26.2. Написать программу для решения задач оптимизации методом сканирования и методом случайного поиска. Шаги h1 и h2 для метода сканирования выбрать самостоятельно. Проанализировать результаты

Таблица 26.1

№	Критерий	x1	x2	x3	Ограничения
	y®max	[15;70]	[100;170]	[10;20]	x1+x2<150
	y®min	[20;50]	[80;140]	[30;50]	x2+x3>135
	y®max	[30;70]	[100;150]	[12;20]
	y®max	[50;80]	[150;180]	[15;30]	x1+x2-x3>200
	y®min	[20;50]	[100;170]	[20;30]
	y®max	[40;60]	[10;30]	[2,1;2,4]	x1+x2<80
	y®min	[30;70]	[100;150]	[15;25]	x2+x3<155
	y®max	[2;4]	[0,1;0,8]	[40;70]
	y®max	[330;350]	[10;20]	[15,16]	x1+x3>350
	y®min	[20,50]	[90;170]	[10;30]
	y®max	[40;70]	[100;170]	[20;40]	x1+x2<220
	y®min	[30;50]	[80;140]	[15;45]	x2+x3>100
	y®max	[20;70]	[90;150]	[2,26]
	y®max	[50;80]	[100;140]	[15;35]	x1+x2+x3>175
	y®min	[0,8;1,6]	[0,3;0,8]	[1,6;2,5]

Таблица 26.2

№	Математическая модель
	y=48,94+9,29x1-3,26x2+8,41x3-0,76x1x2-2,44x1x3-8,24x2x3
	y=21,93+4,56x1+7,76x3-0,69x1x2-0,44x2x3
	y=23,63+4,65x1-2,15x2+5,68x3-1,03x1x2-5,6x2x3
	y=75,78+5,13x1+7,15x3-0,65x1x3-3,58x2x3
	y=21,77+2,97x1+4,23x3-0,51x1x2-2,1x2x3
	y=3,59+0,69x1-1,36x2+0,66x3+0,26x1x3
	y=40,28+8,98x1-3,27x2+10,95x3-0,68x1x2-1,71x1x3-8,65x2x3
	y=2100-665,4x1-242,9x1x2+115,4x1x3-67,1x2x3
	y=26,36+0,89x1-2,01x2+1,89x3-1,19x1x2+1,01x2x3
	y=48,43+8,98x1-3,3x2+8,7x3-1,35x1x2-1,85x1x3-8,13x2x3
	y=22,73+4,65x1-1,28x2+10,08x3-0,95x1x2+0,55x1x3-1,48x2x3
	y=34,67+6,18x1+x2+10,45x3+1,95x1x2-2,5x1x3-5,28x2x3
	y=23,8+4,68x1-2,13x2+5,68x3-0,95x1x2-0,45x1x3-5,6x2x3
	y=18,14+3,69x1-1,09x2+5,44x3-0,14x1x2-1,16x1x3-3,89x2x3
	y=16,79+0,61x1-3,2x2+0,41x3-0,6x1x2-0,2x1x3-0,24x2x3

Рассмотрим дифференциальное уравнение первого порядка:

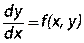(27.1)

Требуется найти решение на интервале [x₀,x_n], удовлетворяющее начальному условию y(x₀)=y₀.

Для приближённого решения дифференциального уравнения (27.1) интервал [x₀,x_n] разбивается на n частей с шагом h:

x_i+1=x_i+h, i=0,1,2,…,n-1 (27.2)

В полученных точках вычисляются значения y_i.

Метод Эйлера. Согласно методу Эйлера значения y_i определяются по формуле:

y_i+1=y_i+h×f(x_i,y_i) (27.3)

Алгоритм метода Эйлера

1. Ввод n, конечного значения x_n, начального значения x₀ (в переменную x ), ввод y₀ (в переменную y ).

2. Вычисление h= , x=x₀, y=y₀.

3. Вывод x, y.

4. Вычисление y=y+h×f(x,y), x=x+h.

5. Если x>x_n, то переход к 6, иначе – переход к пункту 3.

6. Конец вычислений.

Для получения достоверных результатов значение h должно быть достаточно мало, при этом можно не выводить все получающиеся значения x и y. Целесообразно внести изменения в алгоритм программы так, чтобы вычисления проводились с малым шагом, а вывод результатов − с большим.

Метод Рунге-Кутта. Расчетные формулы метода Рунге-Кутта четвертого порядка имеют вид:

k1=h×f(x_i,y_i)

k2=h×f(x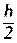_i+, y_i+)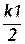

k3=h×f(x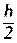_i+, y_i+)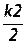

k4=h×f(x_i+h, y_i+k3)

y_i+1=y_i+×(k1+2×k2+2×k3+k4) (27.4)

x_i+1=x_i+h, i=0,1,2,…, n-1

Для разработки программы, реализующей метод Рунге-Кутта можно использовать тот же алгоритм, что и для метода Эйлера, внеся в него соответствующие изменения.

Дата добавления: 2014-01-20