Математические модели сложных измерительных сигналов

А б

А б

Математические модели элементарных измерительных сигналов

К элементарным измерительным сигналам относятся постоянный во времени сигнал и сигналы, описываемые единичной и синусоидальной функциями, а также дельта-функцией.

Постоянный сигнал - самый простой из элементарных сигналов, описываемый математической моделью вида U = А, где А - единственный параметр сигнала. Графики временной и частотной моделей постоянного сигнала приведены на рисунке 16

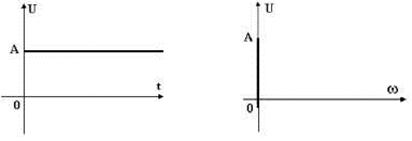
Рисунок 16 - Графики временной (а) и частотной (б) моделей постоянного сигнала

Единичная функция, называемая иногда функцией Хевисайда, описывается уравнением

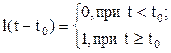
Она имеет один параметр момент времени . Ее временная и частотная модели представлены на рисунке 17,а.

Дельта-функция описывается уравнением

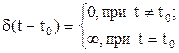
Она также имеет один параметр момент времени . Графики временной и частотной моделей дельта-функции S(t) показаны на рисунке 17,б. Из них видно, что дельта-функция имеет спектр бесконечной ширины.

Дельта-функция обладает следующим свойством:

где ε - любое, сколь угодно малое число.

Она может рассматриваться как предельная функция однопараметрического семейства непрерывных функций, например,нормального распределения с бесконечно малым средним квадратическим отклонением (СКО) σ:

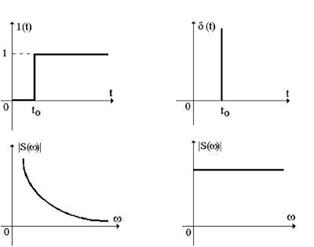
Рисунок 17- График моделей единичной (а) и дельта-функции (б)

Единичная и дельта функции связаны между собой следующими выражениями:

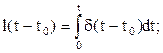
Важной особенностью дельта-функции является стробирующее действие, которое описывается уравнением:

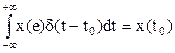
Оно используется для представления дискретизированной во времени функции с шагом дискретизации ∆ t: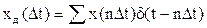

Гармонический сигнал описывается уравнением:

Параметрами такого сигнала являются: амплитуда U_m, период Т (или частота f = 1/T, или круговая частота ω и начальная фаза φ. График временной модели общеизвестен, а график частотной модели такого сигнала показан на рисунке 18.

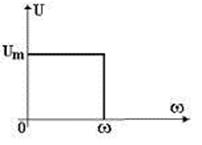
Рисунок 18 - Спектр гармонического сигнала

В средствах измерений используется большое число измерительных сигналов, имеющих самые разнообразные формы. Рассмотрим некоторые из них, наиболее часто встречающиеся на практике.

Прямоугольные импульсы. Одиночный идеальный прямоугольный импульс (рисунок 19,а ) описывается уравнением

,

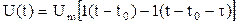т.е. он формируется как разность двух единичных функций, сдвинутых во времени на величину τ - длительность импульса.

Дата добавления: 2014-01-20