Модулированные и детектированные сигналы

А в

Рисунок 19 - Формирование идеального прямоугольного импульса (а),

последовательность прямоугольных импульсов (б)

и трапецеидальный импульс (в)

Последовательность прямоугольных импульсов есть сумма одиночных импульсов:

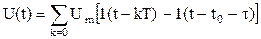
Для ее описания необходимо знать три параметра: амплитуду U_m, длительность τ и период Т (рисунок 19,б). Отношение периода к длительности прямоугольного импульса называется скважностью, а обратная величина -коэффициентом заполнения. При скважности, равной двум, последовательность импульсов называют меандром (см. рисунок 19,б).

Идеальные прямоугольные импульсы в природе не встречаются. В реальных импульсах время изменения сигнала от нулевых до амплитудных значений (и обратно) всегда имеет конечную длительность, т.е. фронт и спад (рисунок 19,в). Следовательно, у реальных импульсов будет трапецеидальная форма.

Трапецеидальный импульс также является идеализацией реальных импульсов, которые имеют гораздо более сложную форму. Она отличается от трапеции спадом вершины импульса, выбросами на вершине и в паузе и другими особенностями, учтенными в системе параметров реального прямоугольного импульса.

Сигналы с линейными участками. При построении средств измерительной техники широкое применение находят периодические сигналы с линейными участками. Это прежде всего линейный знакопеременный и однополярный линейно изменяющийся (пилообразный) сигналы (рисунок 20). Линейный знакопеременный сигнал описывается уравнением

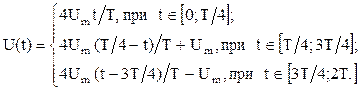
Пилообразный сигнал, при .

а б

Рисунок 20 - Линейный знакопеременный (а) и однополярный линейно изменяющийся (пилообразный) (б) сигналы

Модулированным называется сигнал, являющийся результатом взаимодействия двух или более сигналов, т.е.модуляции. Модуляция - это воздействие измерительного сигнала Х(t) на какой-либо параметр стационарного сигнала U(t), обладающего такими физической природой и характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала, именуемого несущим, обычно выбирают синусоидальное (гармоническое) колебание

(1)

или последовательность импульсов.

Физически процесс, обратный модуляции, называется демодуляцией, или детектированием, и заключается в получении из модулированного сигнала другого сигнала, пропорционального модулирующему. Задача демодуляции -по возможности полное восстановление информации, содержащейся в модулирующем сигнале X(t).

Вид модуляции и способ детектирования зависят от требований, предъявляемых к точности передачи информации. Наиболее простым модулированным гармоническим сигналом является амплитудно-модулированный сигнал, в котором измерительная информация содержится в амплитуде несущего синусоидального сигнала (рисунок 21).

Рисунок 21 - Амплитудно-модулированный(1) и модулирующий (2) сигнал

Амплитудно-модулированные сигналы описываются формулой;

где m - глубина амплитудной модуляции (всегда меньше единицы). При частотной модуляции (рисунок 22) измерительная информация содержится в частоте модулированного сигнала, т.е.

,

где 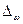- наибольшее изменение частоты модулированного сигнала, т.е. девиация частоты, пропорциональная амплитуде модулирующего сигнала.

При фазовой модуляции (рисунок 23) модулирующий сигнал X(t) воздействует на фазу несущего колебания:

где - коэффициент фазовой модуляции.

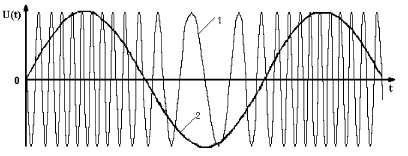
Рисунок 22 - Частотно-модулированный (1) и модулирующий (2) сигналы

Для того чтобы при детектировании можно было восстановить модулирующий сигнал, необходимо иметь сигнал, определяемый выражением (1) и называемый опорным. Относительно него наблюдают, как меняется фаза модулированного сигнала. Модулирующий, фазомодулированный и опорный сигналы показаны на рисунке 23.

Рисунок 23 - Модулирующий (1), фазомодулированный (2)

и опорный (3) сигналы

Если модулируемым сигналом является периодическая последовательность прямоугольных импульсов, то возможны следующие три вида модуляции (рисунок 24):

- амплитудно-импульсная (АИМ);

- частотно-импульсная (ЧИМ);

- широтно-импульсная (ШИМ).

При этом параметром, несущим измерительную информацию, соответственно являются амплитуда, частота и длительность импульсов.

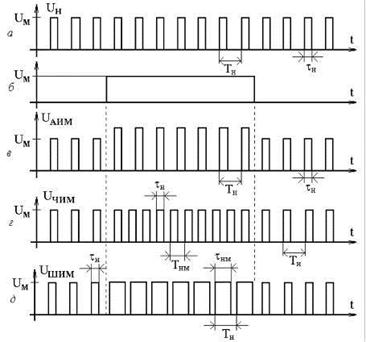
Рисунок 24 - Несущая последовательность прямоугольных импульсов (а),

модулирующий (б), амплитудно-модулированный (в), частотно-модулированный (г) и широтно-модулированный (д) сигналы

Дата добавления: 2014-01-20