
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вероятностное описание случайных погрешностей
|
|
|
|
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
Присутствие случайных погрешностей в результатах измерений легко обнаруживается из-за их разброса относительно некоторого значения. Как уже отмечалось ранее, и результат измерения, и его погрешность с известными оговорками могут рассматриваться как случайные величины.
Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения. Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина хi в i-м опыте принимает значение, меньшее х:
F(X) = Р {Хi < X} = Р{ - < Xi < = Х }.
< Xi < = Х }.
График интегральной функции распределения показан на рис.5. Она имеет следующие свойства:
• неотрицательная, т.е. F(x) > О;
• неубывающая, т.е. F(x2) > F(x1), если х2 >= х1;
• диапазон ее изменения простирается от 0 до 1, т.е. F(- ) =0;
) =0;
F(+ ) = 1;
) = 1;
• вероятность нахождения случайной величины х в диапазоне от x1 до х2 Р{х1 < х < х2} = F(x2) - f(x1).
Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей р(х) = dF(x)/dx. Она всегда неотрицательна и подчиняется условию нормирования в виде:
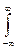 p(x)dx = 1
p(x)dx = 1
Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х1; х2)
P{x1 < x < x2} =  p(x)dx
p(x)dx
Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [-∞;∞] равна единице, т.е. представляет собой достоверное событие.
Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (х1;x2) равна площади, заключенной под кривой р(х) между абсциссами х1 и х2 (см. рис.5). Поэтому по форме кривой плотности вероятности р(х) можно судить о том, какие значения случайной величины х наиболее вероятны, а какие наименее.
Результирующая погрешность зачастую складывается из ряда составляющих с различными плотностями распределения р1(Х), р2(х),..., рn(х). В связи с этим возникает задача определения суммарного закона распределения погрешности. Для суммы независимых непрерывных случайных величин х1 и х2, имеющих распределения р1(x) и р2(х), он называется композицией и выражается интегралами свертки
:
Р(z) = 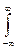 р1(х1)р2(z-x1)dx1 =
р1(х1)р2(z-x1)dx1 = 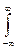 р1(z-x2)p2(x2)dx2.
р1(z-x2)p2(x2)dx2.
Графическое определение композиции двух случайных независимых величин показано на рис. 6. Следует отметить, что масштаб всех графиков по вертикали произвольный, и должно выполняться условие: площадь, ограниченная кривой плотности вероятности, равна единице.

Рис.5. Интегральная (а) и дифференциальная (б) функции
распределения случайной величины.
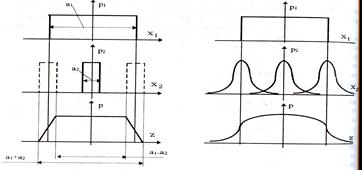
Рис.6. Суммирование законов распределения
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1156; Нарушение авторских прав?; Мы поможем в написании вашей работы!