Суммирование систематических погрешностей

При определении границ систематическая погрешность оцени­вается по ее составляющим, называемым элементарными систематическими погрешностями. Если для части составляющих на­ходят их оценки и эти погрешности устраняют введением поправок, то в качестве рассматриваемых элементарных погрешностей выступают погрешности определения поправок, которые также характеризуются границами.

Множество возможных способов измерений данной величины дает множество различных реализаций каждой элементарной систематической погрешности. Поэтому последние можно рассматривать как случайные величины и суммировать методами, разработанными в математической статистике. Однако поскольку их функции распределения, как правило, неизвестны, то при суммировании видом распределения задаются, исходя из известных данных об элементарной систематической погрешности. Это не вносит существенной ошибки в получаемые результаты, так как в соответствии с принципом оценивания погрешностей сверху из всех возможных ее распределений всякий раз выбирают наихудшее. Получаемая оценка погрешности надежно характеризует неопределенность результата.

При выборе закона распределения необходимо руководствоваться следующими правилами:

• если известна оценка границ погрешности ±θ_i, то ее распреде­ление следует считать равномерным (такая ситуация наиболее час­то встречается в практике);

• если известна оценка СКО, то распределение следует считать нормальным.

Применение этого правила позволяет статистически суммиро­вать элементарные систематические погрешности и обычно приво­дит к осторожным и вместе с тем не слишком завышенным оцен­кам погрешности результата измерений.

При равномерном законе распределения элементарных систе­матических погрешностей их сумма

, если < ,

, если >= ,

где θ_i — границы i-й элементарной случайной погрешности; k —попра­вочный коэффициент, зависящий от числа слагаемых m, их соотноше­ния и доверительной вероятности. При Р < 0,99 он мало зависит от числа слагаемых и может быть представлен усредненными значения­ми. Их погрешность не превышает 10%.

При Р >= 0,99 коэффициент k существенно зависит от числа слагаемых и соотношения между ними. Поэтому при m > 4 рекомендуется принимать среднее значение k = 1,4, а при m <= 4 значение k необходимо уточнить по ГОСТ 8.207-76. Параметр С, характеризующий отношение границ составляющих систематической погрешности θ_m/θ_m-₁, принимается равным наименьшему зна­чению указанного отношения при условии, что θ₁ <= θ₂ <= θ₃ <= θ₄.

При большом числе слагаемых результирующая погрешность имеет практически нормальное распределение. Оценка дисперсии этого распределения равна сумме дисперсий слагаемых:

S²_θ = 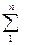θ_i²/3.

Задавшись доверительной вероятностью, получим θ как гра­ницу доверительного интервала θ = Z_pS_θ, где Z_p — квантиль нор­мального распределения при выбранном уровне значимости q = 1-Р.

Дата добавления: 2014-01-20