Замечание 3. Вероятность попадания нормированной нор­мальной величины Х в интервал (0, х) можно найти, пользуясь

Замечание 4.

и, следовательно, в силу симметрии φ (x) относительно нуля

легко получить, что

Действительно,

Нормальная кривая

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию

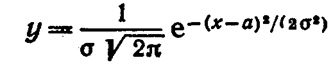методами дифференциального исчисления.

1. Очевидно, функция определена на всей оси Ох.

Рис. 1

Рис.1. Нормальная кривая при а == 1 и

2. При всех значениях х функция принимает поло­жительные значения, т. е. нормальная кривая располо­жена над осью Ох.

3. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю:

ось Ох служит горизонтальной асимптотой графика.

4. Исследуем функцию на экстремум. Найдем первую производную:

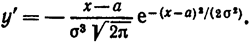
Следовательно, при х==а функция имеет максимум равный:

5. Разность х — а содержится в аналитическом выра­жении функции в квадрате, т.е. график функции сим­метричен относительно прямой х = а.

6. Исследуем функцию на точки перегиба. Найдем вторую производную:

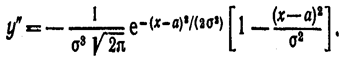
Легко видеть, что при и 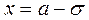вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции

На рис. 1 изображена нормальная кривая при а == 1 и

Влияние параметров нормального

распределения на форму нормальной кривой

Выясним, как влияют на форму и расположение нормальной кривой значения параметров а и 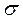. Известно, что графики функций и 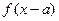имеют одинаковую форму.Сдвинув график в положительном направлении оси Ox на а единиц масштаба при а > 0

или в отрицательном направ­лении при а < 0, получим график f (x - a ).

Отсюда сле­дует, чтоизменение величины параметра «а » (математиче­ского ожидания) не изменяет формы нормальной кривой, а приводит лишь к её сдвигу вдоль оси Ох: вправо, если «а» возрастает, и влево, если «а» убывает.

По-иному обстоит дело, если изменяется параметр σ (среднее квадратическое отклонение). Как было указано в предыдущем параграфе, максимум дифференциальной функции нормального распределения равен 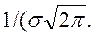Отсюда следует, что с возрастанием 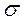максимальная ордината нормальной кривой убывает, а сама кривая стано­вится более пологой, т. е. сжимается к оси Ох: при убывании 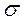нормальная кривая становится более «островершинной·» и растягивается в положительном направле­нии оси Оу.

Подчеркнем, что при любых значениях параметров а и s площадь, ограниченная нормальной кривой и осью х, остается равной единице (см., второе свойство плотности распределения).

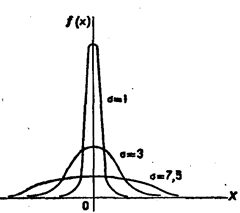
Рис.2.

На рис. 2 изображены нормальные кривые при раз­личных значениях σ и а = 0. Чертеж наглядно иллюстри­рует, какизменение параметра σ сказывается на форме нормальной кривой.

Заметим, что при а = 0 и σ = 1 нормальную кривую называют нормированной:

2. Вероятность попадания в заданный интервал нормальной случайной величины. Вычисление вероятности заданного отклонения.

Уже известно, чтоесли случайная величина Χ задана плотностью распределения f (x), то вероятность того, что Χ примет значение, принадлежащее интервалу (α, β), равна:

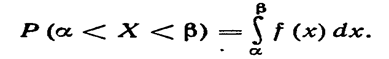
Пусть случайная величина Χ распределена по нор­мальному закону.Тогда вероятность того, что Χ примет значение, принадлежащее интервалу (α, β),равна

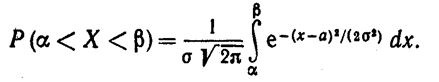
Преобразуем эту формулу так, чтобыможно было пользоваться готовыми таблицами. Введем новую переменную 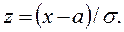Отсюда Найдём новые пределы интегрирования. Так, если то 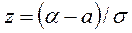, если 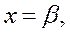то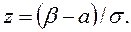

Таким образом, имеем

Пользуясь функцией Лапласа

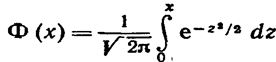
окончательно получим

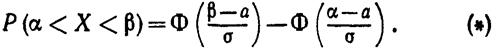Пример. Случайная величина Χ распределена по нормальному закону. Математическое ожидание и среднее квадратическое откло­нение этой величины соответственно равны 30 и 10. Найти вероят­ность того, что Χ примет значение, принадлежащее интервалу (10, 50).

Решение. Воспользуемся формулой (*). По условию a=10,

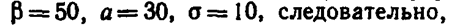
По таблице приложения №1 находим Φ (2) == 0,4772. Отсюда иско­мая вероятность

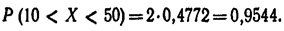
Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной вели­чины Χ по абсолютной величине меньше заданного по­ложительного числа δ, т. е. требуется найти вероятность осуществления неравенства:

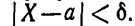
Заменим это неравенство равносильным ему двойным неравенством

Пользуясь формулой вычисления вероятности попадания нормально-распределённой случайной величины в заданный интервал, получим

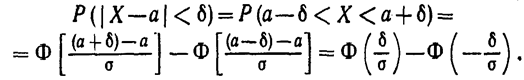
Приняв во внимание равенство

(функция Лапласа—нечетная), окончательно имеем

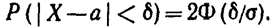
В частности, при а = 0

На рис. 3 наглядно показано, что если две случайные величины нормально распределены и а = 0, товероятность принять значение, принадлежащее интервалу (— δ, δ),

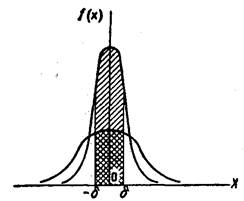
Рис.3.

больше у той величины, кото­рая имеет меньшее значение σ.

Этот факт полностью соответ­ствует вероятностному смыслу параметра σ

(σ есть среднее квадратическое отклонение; оно характеризует рассеяние

слу­чайной величины вокруг ее математического ожидания).

Замечание. Очевидно, что со­бытия, состоящие в осуществлении неравенств

и - противоположные. Поэтому, если вероятность

осуществления неравенства равна , товероятность неравенства

равна .

Пример.Случайная величина Х распределена нормально. Мате­матическое ожидание и среднее квадратическое отклонение Χ соот­ветственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

Решение.Воспользуемся формулой вычисления вероятности заданного отклонения

По таблице приложения №1 находим Φ (0,3) =0,1179. Тогда, искомая вероятность:

Правило трех сигм

Преобразуем формулу по вычислению вероятности заданного отклонения:

положив . В итоге получим:

Если 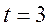и, следовательно, то

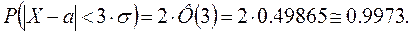
Т. е.вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала,а именно равна 0,0027.Это означает, чтолишь в 0,27% случаев так может произойти.

Такие события, исходя из принципа невозмож­ности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно,но условие, указанное в приведенном правиле, выпол­няется, то есть основание предполагать, чтоизучаемая величина распределена нормально; в противном случае она не распределена нормально.

3. Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс

Эмпирическим называют распределение относи­тельных частот. Эмпирические распределения изучает математическая статистика.

Теоретическим называют распределение вероятностей. Теоретические распределения изучает теория вероятностей. В этой лекции рассматриваются теоретические распре­деления.

При изучении распределений, отличных от нормаль­ного,возникает необходимость количественно оценить это различие. С этой целью вводят специальные числовые характери­стики СВ,в частностиасимметрию и эксцесс.

Для нормаль­ного распределения эти характеристики (асимметрия и эксцесс)равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предпо­ложить близость этого распределения к нормальному, и наоборот, большие значения асимметрии и эксцесса ука­зывают на значительное отклонение этого распределения от нормального.

Как оценить асимметрию?Можно доказать, чтодля симметричного распределения (график такого распреде­ления симметричен относительно прямой x = Μ (Χ)) каждый центральный момент нечетного порядка равен нулю.

Для несимметричных распределенийцентральные моменты не­четного порядка отличны от нуля. Поэтомулюбой из этих (нечётных) моментов(кроме момента первого порядка, который равен нулю для любого распределения) может служить для оценки асимметрии.

Естественно,лучше (проще)выбрать простейший из них,т.е. центральный момент третьего порядка Однако, принять этот момент для оценки ассиметрии не совсем удобно, потому, что его величина зависит от единиц измерения, в которых измеряется случайная величина.Чтобы устранить этот недостаток(оценивать асимметрию безразмерной величиной), 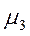делят на и, таким образом, получают безразмерную числовую характеристику

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

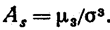
Асимметрия положительна, если «длинная часть» кри­вой распределения расположена справа от математического ожидания; асимметрия отри­цательна,если «длинная часть» кривой расположена слева от математического ожидания.

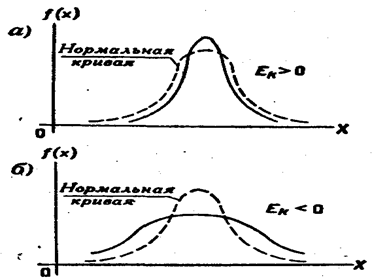
Практически оп­ределяют знак асимметрии по расположению кривой рас­пределения относительно мо­ды (точки максимума диффе­ренциальной функции): если «длинная часть» кривой рас­положена правее моды,то асимметрия положительна(рис. 4, а), если «длинная часть» кривой слева— то асимметрия отрицательна (рис.4 б).

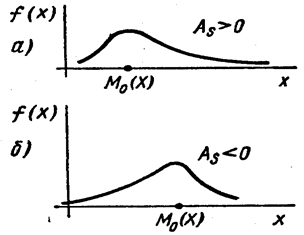
Рис.4.

Для оценки «крутости» кривой распределения,т. е. большего или меньшей подъема кривой теоретического распределения по сравнению с нормальной кривой,пользуются такой характеристи­кой, какэксцесс.

Эксцессом теоретического распределения называют ха­рактеристику, которая опре­деляется равенством:

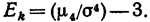
Для нормального распределения 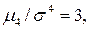следовательно, эксцесс равен нулю. Поэтому если экс­цесс некоторого распре­деления отличен от нуля, то кривая этого распределения отличается от нормальной кривой:если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая (рис. 5, α);если эксцесс отрицательный, то сравниваемая кривая имеет более низ­кую и «плоскую» вершину, чем нормальная кривая (рис. 5,б).При этом предполагается, чтонормальное и теоретическое распределения имеют одинаковые матема­тические ожидания и дисперсии.

Рис.5.

4. Центральная предельная теорема (теорема Ляпунова)

Известно, что нормально распределенные случай­ные величины широко распространены на практике. Чем это объясняется?Ответ на этот вопрос был дан выдаю­щимся русским математиком А. М. Ляпуновым (централь­ная предельная теорема):если случайная величина X пред­ставляет собой сумму очень большого числа взаимно неза­висимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.

Пример.Пусть производится измерение некоторой физической величины. Любое измерение дает лишь приближенное значение изме­ряемой величины, так как на результат измерения влияют очень многие независимые случайные факторы (температура, колебания прибора, влажность и др.). - Каждый из этих факторов порождает ничтожную «частную ошибку».Однако, поскольку число этих факторов очень велико, их совокупное действие порождает уже заметную «суммар­ную ошибку». Рассматривая Суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок,мы вправе заключить, чтосуммарная ошибка имеет распределение, близкое к нормальному.Опыты подтверждают справедливость такого заключения.

Приведем формулировку центральной предельной тео­ремы, которая устанавливает условия, при которых сумма большого числа независимых слагаемых имеет распреде­ление, близкое к нормальному.

Пусть X₁, X₂ ,... Х_п , — последовательность неза­висимых случайных величин,

каждая, из которых имеет конечные математическое ожидание и дисперсию:

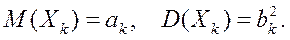
Введем обозначения:

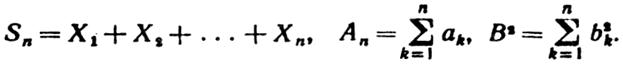
Обозначим функцию распределения нормированной суммы через:

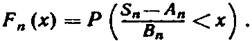Говорят, чток последовательности X₁ , X₂ ,. .. приме­нима центральная предельная теорема,если при любом хфункция распределения нормированной суммы при п ® ∞ стремится к нормальной функции распределения:

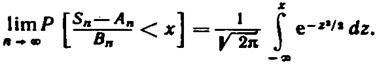
В частности, если все случайные величины Х₁ , X₂ ,... одинаково распределены,то к этой последовательности применима центральная предельная теорема,если диспер­сии всех величин X _i ( i = 1, 2,...) конечны и отличны от нуля.

А. М. Ляпунов доказал, чтоесли для > 0 при п ® ∞ отношение Ляпунова

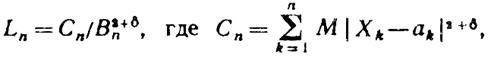
стремится к нулю(условие Ляпунова),то к последова­тельности Х_1, X₂, ... применима центральная предельная теорема.

Сущность условия Ляпуновасостоит в требовании, чтобыкаждое нормированной слагаемое суммы (S_n — А_n)/В_n оказывало на сумму ничтожное влияние.

Замечание. Для доказательства центральной предельной тео­ремы А. М. Ляпунов использовалаппарат характеристических функ­ций.Характеристической функцией случайной величины Xназываютфункцию .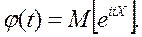

Для дискретной случайной величины Xс возможными значениями и их вероятностями характеристическая функция

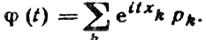
Для непрерывной случайной величины Xс плотностью распре­деления f (х)характеристическая функция

Можно доказать, чтохарактеристическая функция суммы неза­висимых случайных величин равна произведению характеристических функций слагаемых.

Автор: к.т.н., доцент В.Е.Куприянов

30.08.2012г.

Приложение №1

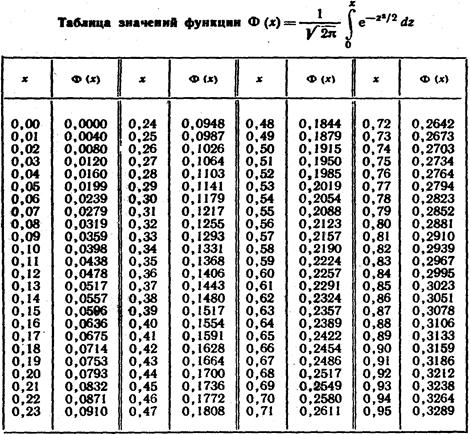
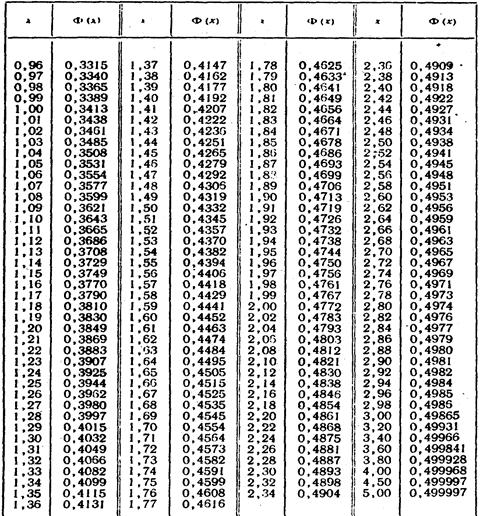
Дата добавления: 2014-01-20