Сформулируем задачу компоновки

Необходимо скомпоновать L-подсхем, каждая из которых должна иметь 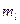внешних выводов. В этом случае задача ставится следующим образом, необходимо разбить E на L-подмножеств таким образом, чтобы достигался некоторый оптимум критерий качества (1,2,3,4).

Решением этой задачи должна быть матрица (N*L) X состоящая 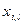, элементы которой определяют следующим образом:

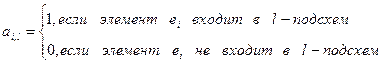
l – количество элементов 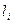части подсхемы, определяется как сумма элементов в матрице x

Введём целочисленную переменную

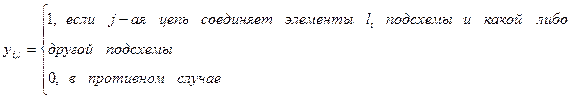
Тогда количество внешних выводов 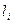подсхемы определяется, как сумма этой целочисленной переменной:

В этом случае суммарное количество внешних выводов всех подсхем будет определятся из следующего уравнения:

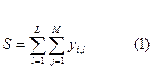
R – число межмодульных соединений

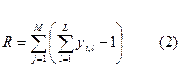
Из уравнений 1 и 2 видно, что уменьшение показателя (сумм количества внешних выводов) ведёт к уменьшению показателя R и наоборот.

Исходя из всего этого можно сказать, что целочисленная переменная будет определятся следующим образом:

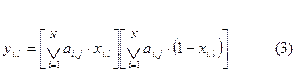
Учитывая уравнения 1 и 3 задача линейного целочисленного программирования формулируется так.

Найти значения элементов матрицы х при которых обеспечивался бы минимум суммарного количества внешних выводов, т.е.

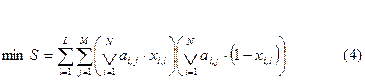
А также минимум числа межмодульных соединений:

При следующих ограничениях:

1. На количество элементов в схеме
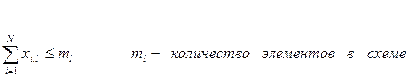
2. На количество выводов подсхем

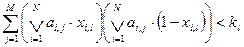
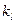- количество внешних выводов

При такой постановке задача имеет значение вычислительной трудности, поэтому для её решения используют приближённые алгоритмы на основе графов.

Пусть схема задана гиперграфом

Х – множество вершин (элементов схемы)

U – множество рёбер (связи между ними)

Тогда задача компоновки схемы в L подсхем ставится как задача разбиения множества X на l подмножеств, где 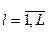, так чтобы оптимизировать некоторую целевую функцию.

Пусть гиперграф задан в виде множества вершин:

При этом задано многозначительные отображение множества вершин в множество рёбер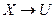

Когда суммарное количество внешних выводов будет определятся по следующему правилу:

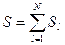
Пример:

Дана схема элементов

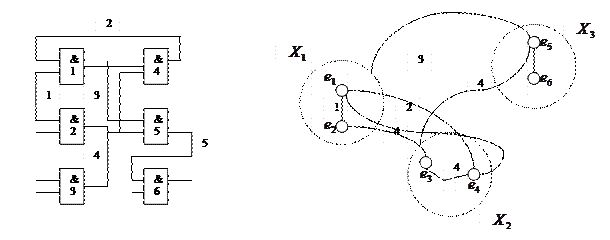
В соответствии с нашим гиперграфом схемы мы имеем множество Х состоящих из следующих вершин:

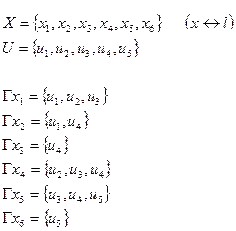
Для компоновки схемы в 3 узла будет верно:

Тогда этим множествам соответствуют следующие рёбра:

На основании приведённых уравнений, число внешних выводов частей схемы будет равно:

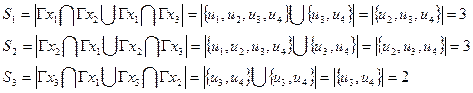
Суммарное количество внешних выводов:

Число межмодульных соединений:

R=5

Вывод: точное решение задачи компоновки в приведённых подстановках возможно лишь методом полного перебора, поэтому практическое применение находит последовательный и итерационный алгоритмы компоновки.

Дата добавления: 2014-01-20