Последовательный алгоритм компоновки

Идея последовательного алгоритма компоновки по связности заключается в следующем:

Выбирается некоторый исходный элемент схемы, из которого сначала и состоит формирующий узел (выбор начального элемента основывается на схемотехнических соображениях) далее к этому узлу присоединяется один или несколько элементов, чей выбор осуществляется по правилу, которое учитывает связность элементов исходного узла с элементами ещё не включёнными в него. Процедура продолжается до тех пор пока выполняется ограничение по числу элементов или числу внешних выводов.

Формирование узлов продолжается по принципу последовательного выделения, т.е. сформированный узел удаляют из схемы, а последовательным алгоритмом формируется новый узел. Процесс повторяют до тех пор пока вся схема не будет разбита на требуемое число частей или будет вычислена невозможность этого.

Основные пункты последовательного алгоритма компоновки:

1. Включаем в формируемое подмножество некоторую исходную вершину
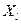
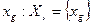
2. По отображению множества рёбер множеству вершин определяем множество рёбер 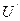, инциндентных этой вершине UàX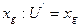
3. По отображению множества вершин в множество рёбер, находим множество вершин 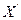, которые входят в эти рёбра и удовлетворяют условиям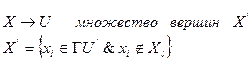

1. Подсчитываем значение показателя S, равное количеству рёбер инциндентным вершинам
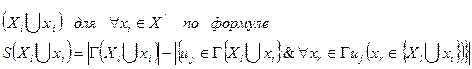
2. Определяем вершину 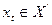, для которой значение S минимальное
3. Проверяем услови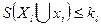е , где 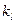-допустимое количество внешних проводов 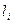части схемы. Если условие выполняется, идём на пункт 7, иначе на пункт 10.
4. Вершину 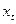включаем в формируемое множество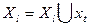
5. После этого проверяем услови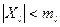е , где 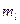- требуемое количество элементов в 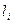части схемы. Если условие выполняется, идём на пункт 9, иначе на пункт 11.
6. Корректируем множество рёбер 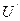, инциндентных вершинам множества 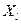. Для этого определяем рёбра 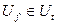, множество вершин которых удовлетворяет следующему условию: 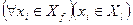или 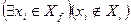. Такие рёбра соответственно удаляются из множества 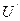или добавляются. Переход на пункт 3.
7. Дальнейшее формирование подмножества 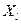невозможно из-за нарушения ограничения по числу внешних проводов. Переход на пункт 12.
8. Подмножество 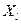сформировано полностью.
9. Конец работы алгоритма

Пример:

Дата добавления: 2014-01-20