Размещение (постановка задачи, критерии оптимизации)

Суть задачи размещения заключается в определении оптимального положения элементов, а также связи между ними в монтажном пространстве.

При удовлетворении конструкторско-технических ограничений:

– Зоны запрещённого монтажа (трассировки)

Все алгоритмы размещения сводятся в следующие группы:

– Алгоритмы решения задач математического программирования

– Последовательные алгоритмы размещения

– Итерационные алгоритмы размещения

– Алгоритмы, использующие непрерывные дискретные методы оптимизации

Исходные данные для постановки задачи размещения:

– Схема соединений элементов, метрические и топологические свойства монтажного пространства

– Имеется множество конструктивных элементов

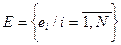, где N – число элементов

– Множество соединяющих их цепей

– Монтажное пространство определено, как множество фиксированных позиций для установки элементов

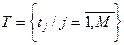, где М – количество позиций (обычно принимают N=M, если M>N, то определяют фиктивные элементы)

Найти такое отображение E à T, при котором достигался бы экстремум целевой функции F.

При этом используют следующие критерии определения качества решения задачи размещения:

1. Минимум суммарной длины всех соединений
2. Минимум длины самой длинной связи
3. Минимум числа пересечений
4. Максимум числа цепей с возможно более простой конфигурацией
5. Максимально близкое расположение модулей, имеющих наибольшее количество связей между собой.

Будем считать, что соединение, исходящее из геометрических центров конструктивных элементов, где расстояние по горизонтали и вертикали одинаково. По данной математической модели монтажного пространства, будет граф решётка 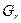, а расстояние между позициями определяется матрицей расстояний 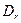. Внешним выводам элементов поставим в соответствии элемент 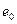, а соединение с ним элементов их множества E учтём вектором столбцов взвешенных связей.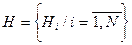

Контактные площадки (кроме разъёмов) инвариантны. Тогда для некоторого размещения суммарная взвешенная длина соединений будет равна:

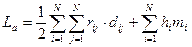
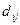- элемент матрицы 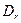, который определяет расстояние между позициями установк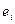и и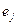

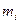- номер вертикального ряда (ордината), в котором расположен элемент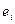

Главная цель размещения – создание наилучших условий для трассировки.

Дата добавления: 2014-01-20