Идея эвристического алгоритма покрытия

Алгоритм решения задачи покрытия

1. Эвристический алгоритм покрытия

Покрытие – это, когда компоновка имеет схемную унификацию.

При описании задачи покрытия, будем считать, что в модулях заданного набора имеются все типы элементов покрываемой схемы. При этом модули элементов условно разбивают на 2 класса:

1. Все входы и выходы являются внешними проводами (состоят из несвязанных элементов)

2. Модули состоят из связанных элементов

Эвристический алгоритм моделирует процесс поиска в схеме подсхемы аналогичной модулю заданного набора элементов. При этом элементы схемы просматриваются и включаются в подсхемы последовательно один за другим. Покрываемая схема представляется взвешенным ориентированным мультиграфом , множество элементов которого сопоставляется вершинам А-связи между элементами множества рёбер.

Каждый модуль заданного набора является совокупностью связанных элементов (i-1)-уровня. При этом интерпретируется ориентированным графом 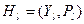, который называется эталоном. Таким образом, заданным наборам элементов сопоставляется множество ориентированных графов , где n – число типов, используемых модулей.

Т.е. при решении задачи покрытия эвристических алгоритмов для каждого эталонного графа 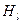, решает задачу его вложения в графсхему G. Если же такой подграф найти не удаётся, то переходим к поиску следующего подграфа .

Процесс повторяют до тех пор пока вся схема не будет покрыта модулями заданного набора или выяснится невозможность этого.

При положительном результате получают вариант состава модулей в виде следующего множества , где - число модулей, используемых для покрытия схемы.

Основное правило эвристического алгоритма:

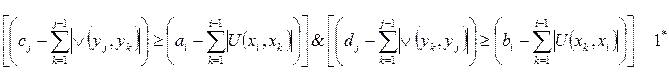
Где - полустепени для исхода и захода для вершины

- полустепени для исхода и захода для вершины

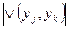- число рёбер выходящих из рассматриваемой вершины эталона в уже просмотренные вершины

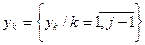
- число рёбер входящих в вершину из вершины

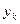
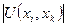- число рёбер выходящих из рассматриваемой вершины графа схемы G, в вершины и включаемых в формируемый подграф

- число рёбер входящих в рассматриваемую вершину графа схемы G из вершины и включаемых в формируемый подграф

Основные пункты эвристического алгоритма покрытия:

1. Проверяем по типам вершин возможность вложения эталонного графа 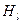в граф схемы G. Т.е. . Если условие выполняется – переход на пункт 2, иначе на пункт 26.

2. Выделяем из графа схемы подмножества вершин , которое удовлетворяет следующему условию: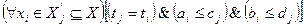

3. Текущую вершину ставим в соответствие вершине

4. Если вершина эталона , является по порядку 1-ой (j=1) – переход на пункт 21, иначе на пункт 5.

5. Определяем обратное отображение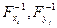

6. Для очередных вершин проверяем выполнение следующего условия:

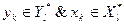. Переход на пункт 8, иначе на пункт 7.

7. Проверяем выполнение условия:

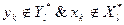. Переход на пункт 10, иначе на пункт 20.

8. Проверяем выполнение следующего условия:

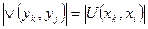. Переход на пункт 9, иначе на пункт 20.

9. Подсчитываем общее количество связей для рассматриваемых вершин с вершинами :

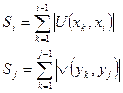
10. Анализируем, все ли вершины из отобранных отображений просмотрены 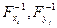, если нет – переход на пункт 6, если да – переход на пункт 11.

11. Для вершини проверяем условие по заходящим рёбрам:

, переход на пункт 12, иначе на пункт 20.

12…18. Проверяем пункты с 5 по 11 для прямого отображения. При выполнении условия 1* по выходящим рёбрам – переход на пункт 21.

19. При не выполнении условия 1* по выходящим рёбрам – переход на пункт 20.

20. Анализируем, все ли вершины из подмножества кандидатов просмотрены , переходим на пункт 24, иначе на пункт 3.

21. Включаем вершину в формируемый подграф , т.е.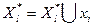

22. Если подграф 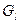не просмотрен полностью, т.е. 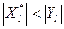, то увеличиваем j на единицу и переходим на пункт 2, иначе на пункт 23.

23. Подграф 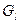идентичный эталонному 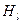сформирован. Переход на пункт 27.

24. Возвращаемся на предыдущий шаг алгоритма и проверяем условие (j-1)=0?. Переход на пункт 26, иначе на пункт 25.

25. Анализируем, все ли вершины из подмножества просмотрены. Переход на пункт 24, иначе 4..20 для (j-1)-шага алгоритма.

26. Подграфа идентичного эталонному графу нет.

27. Конец работы алгоритма.

Дата добавления: 2014-01-20