Общие сведения об эксперименте

5.1 Основные понятия и определения

Независимые переменные величины, влияющие на протека процесса, называются факторами. Факторами могут быть температура, давление, состав реакционной смеси и т. п. Эти величины обозначают буквами х ₁ ,..., х _n.

Протекание процесса количественно характеризуется одной пли несколькими величинами, например, производительностью обору­дования, себестоимостью продукции и т. п. Такие величины в тео­рии планирования эксперимента называют функциями отклика и обозначают буквами у ₁ ,..., у _m. Функции отклика зависит от влияющих факторов, т. е.

у ₁₌ у ₁(х ₁ ,..., х _n) (5.1)

где j — 1,2…, m.

Геометрический образ, соответствующий функции отклика, на­зывают поверхностью отклика (рис. 1). Координатное простран­ство, по осям которого отложены факторы, называют факторным пространством.

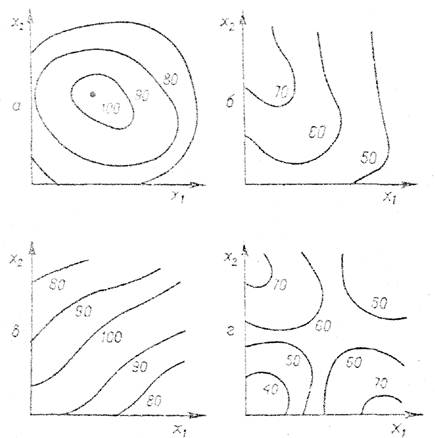
Для удобства рассмотрения поверхность отклика может быть представлена на факторной плоскости (х ₁, х ₂ ) линиями постоян­ных значений функции отклика (аналогично изображению рельефа местности на географических картах). На рис. 2 изображены не­которые типы поверхностен отклика. Здесь в качестве примера функции отклика взята степень чистоты продукта реакции, выраженная в процентах.

На рис. 2, аповерхность отклика имеет вид «вершины» и соот­ветствует области значении факторов, где расположен максимум величины у. Очевидно, аналогичный вид имеют линии постоянного уровня и в случае минимума функции у.

Поверхность, изображенная на рис. 2, б, характеризует плав­ное возрастание функции отклика с уменьшением фактора х ₁ и увеличением х ₂. Такую поверхность принято называть «стационар­ным возвышением». Поверхность, показанная па рис. 2, в, называется «хребтом». Его вершина соответствует наибольшим значениям функции от­клика. Аналогично располагают­ся линии постоянных значении у и в случае «оврага», дно кото­рого соответствует минимальным значениям функции отклика.

Рис.1 Поверхность отклика.

Наконец, на рис, 2, изображена поверхность, называемая «седлом». На двух участках этой поверхности наблюдается возрастание функции отклика, а на двух других – убывание.

Следует отметить, что па практике встречаются поверхности отклика и с более сложной конфигурацией.

Рис. 2. Типы поверхностей отклика.

Если число влияющих факторов больше двух, то для изображения поверхности отклика пользуются ее двумерными сечениями. Сэтой целью каждый раз фиксируют все факторы, кроме двух.

5.2 Проверка воспроизводимости опытов

Прежде, чем приступить к планированию эксперимента, необходимо убедиться в том, что опыты воспроизводимы. Для этой цели проводят несколько серий параллельных опытов в рассматриваемой области изменения влияющих факторов. Результаты этих опытов сводятся в таблице 2.

Таблица 2

Эксперимент для проверки воспроизводимости опытов

Номер серии опытов	Результаты параллельных опытов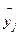
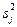
	у11	у12	…	у1k
	у21	у22	…	у2k
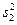
	у31	у32	…	у3k
…	…		…	…	…	…
	уj1	уj2	…	уjk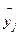
…	…		…	…	…	…
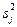
N	уN1	уN2	…	уNk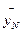

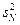
Для каждой серии параллельных опытов вычисляют среднее арифметическое значение функций отклика

(j=1,2,…, N) (5.2)

где k – число параллельных опытов, проведенных при одинаковых условиях.

Обычно N и k берут от 2 до 4.

Затем вычисляют оценку дисперсии для каждой серии параллельных опытов:

(5.3)

для проверки воспроизводимости опытов находят отношение наибольшей из оценок дисперсий к сумме всех оценок дисперсий:

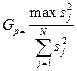(5.4)

Эта величина называется расчетным значением критерия Кохрена.

Значения критерия Кохрена приведены в Приложении 1. Они соответствуют доверительной вероятности Р=0,95, с которой принимается гипотеза о воспроизводимости опытов.

Следует отметить, что величина р=1-Р называется уровнем значимости.

Для нахождения G необходимо знать общее количество оценок дисперсий N и число степеней свободы f, связанных с каждой из них, причем f= k-1.

Если выполняется условие G_p £ G, то опыты считаются воспроизводимыми, а оценки дисперсий – однородными.

Если опыты невоспроизводимы, то можно попытаться достигнуть воспроизводимости выявлением и устранением источников нестабильности эксперимента, а так же использование более точных методов и средств измерений.

Наконец если никакими способами невозможно достигнуть воспроизводимости, то математические методы планирования к такому эксперименту применять нельзя.

Пример 5.1. Рассмотрим эксперимент, в котором измерялся выход продукта реакции y (%), зависящей от двух факторов – температуры x ₁ (°С) и концентрации вещества x ₂ (%). Условия проведения опытов и результаты измерений приведены в таблице 3.

Таблица 3.

Условия проведения опытов и результаты измерений

Номер серии опытов	Условия опытов	Результаты измерений	, %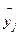
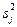
x 1 °С	x 2 %.	уj1, %	уj2, %
			35,0	36,0	35,5	0,50
			39,3	38,7	38,7	0,72
			31,4	32,6	32,6	1,28

Расчетное значение критерия Кохрена находим по формуле:

=

Соответствующее значение критерия Кохрена G=0,967 берем из Приложения 1. Оно найдено для следующих значений параметров: Р=0,95, N=3; f=k=2-1=1.

Условия G_p £ G выполнено, следовательно, опыты можно считать воспроизводимыми.

5.3 Вычисление погрешности эксперимента

Оценки однородных дисперсий нескольких серий параллельных опытов можно усреднить и найти величину

,

называемую оценкой дисперсии воспроизводимости. С ней связано число степеней свободы f= N (k-1).

На основании таблицы 3:

₌

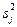f= N (k-1)= 3(2-1)=3

Оценку дисперсии среднего значения рассчитывают по формуле:

(5.7)

С ней также связано число степеней свободы f= N (k-1).

В рассматриваемом примере 5.1

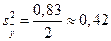
Если при проведении эксперимента опыты дублируют и пользуются средними значениями функции отклика y, то при обработке экспериментальных данных следует использовать s²_y.

5.4 Рандомизация

Для того чтобы в известной мере компенсировать систематические погрешности эксперимента, используют прием, называемый рандомизацией. Он заключается в том, что опыты проводят в случайной последовательности, которая устанавливается с помощью таблицы случайных чисел (см. Приложение 2).

Пусть, например, требуется рандомизировать во времени 6 опытов, обозначенных цифрами I, II,…, VI. Поставим им в соответствии любые 6 последовательных чисел, взятых в любой строке или в любом столбце таблицы приложения 2. Если при этом встретятся повторяющиеся числа, то их следует отбросить.

Например, могут быть получены следующие пары:

I – 60	IV – 15
II – 12	V – 34
III – 05	VI – 30

Расположив случайные числа в порядке возрастания (или убывания), получаем искомую последовательность реализации опытов:

III, II, IV, VI, V, I (или I, V, VI, IV, II, III)

Дата добавления: 2014-01-20