Экспериментально-статистические модели

6.1 Математическое описание

Под математическим описанием процесса будем понимать си­стему уравнении, связывающих функции отклика с влияющими факторами. В простейшем случае это может быть одно уравнение. Часто математическое описание насыпают математической моделью.

С помощью математических методов оптимального планирова­ния эксперимента можно получить математическую модель про­цесса даже при отсутствии сведений о его механизме. Это в ряде случаев бывает очень полезно.

Ценность математического описания заключается в том, что:

во-первых, дает информацию о влиянии факторов;

во-вторых, позволяет количественно определить значения функции отклика при заданном режиме ведения процесса;

в-третьих, может служить основой для оптимизации.

Следует отметить, что на основе методов планирования эксперимента можно количественно описать также свойства таких про­дуктов, как сплавы, пластмассы, резины, керамика, ситаллы, бе­тоны и т. п.

Математические модели, получаемые с помощью методов пла­нирования эксперимента, принято называть экспериментально-статистическими.

6.2 Полный факторный эксперимент

Метод полного факторного эксперимента дает возможность по­лучить математическое описание исследуемого процесса в некото­рой локальной области факторного пространства, лежащей в окрестности выбранной точки с координатами (x ₀₁, x ₀₂,…, x _0n).

Перенесем начало координат факторного пространства в эту точку (рис. 3). С этой целью введем новые переменные

(6.1)

где– масштаб по X_i.

Иногда величину X_i называют кодированной переменной, Функцию отклика в окрестности нового начала координат раз­ложим в ряд Тейлора

у=b₀+b₁ X₁+b₂ X₂+…+b_n X_n+b₁₂ X₁ X₂+…+b_(n-1)n X_n-1X_n+b₁₁X+b₂₂X+b_nnX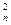+… (6.2)

где b₀= у(0, …, 0) - значение функции отклика в начале координат

, ,

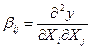и т.д.

Рис. 3. Введение кодированных переменных

Метод полного факторного эксперимента служит для по­лучения математического опи­сания процесса в виде отрез­ка ряда Тейлора (6.2). При этом обычно ограничиваются линейной частью разложения и членами, содержащими про­изведения факторов в первой степени. Таким образом, удается находить уравнение локального участка поверхности отклика, если его кривизна не слишком велика.

Следует отметить, что коэффициенты искомого уравнения определяются на основе экспериментальных данных и, следова­тельно, несут па себе отпечаток погрешностей эксперимента. Чтобы подчеркнуть это обстоятельство, в уравнении вместо симво­лов β обозначающих истинные значения коэффициентов, пишут b, подразумевай под этим соответствующие выборочные оценки.

Итак, с помощью полного факторного эксперимента ищут ма­тематическое описание процесса в виде уравнения:

(6.3)

Его называют уравнением регрессии, а входящие в него коэффи­циенты — коэффициентами регрессии.

Для удобства вычислений коэффициентов регрессии все факоторы в ходе полного факторного эксперимента варьируют на двух уровнях, соответствующих значениям кодированных переменных + 1 и – 1.

Таким образом, полным факторным экспериментом называется система опытов, содержащая все возможные неповторяющиеся комбинации уровней варьирования факторов.

В табл. 4 приведены условии опытов полного двухфакторного эксперимента. Часть таблицы, обведенная пунктиром, называется матрицей планирования.

Таблица 4.

Полный двухфакторный эксперимент.

Номер опыта	Факторы	Функция отклика
x 1	x 2
	-1   +1   -1   +1	-1   -1   +1   +1	y1
	y2
	y3
	y4

Рис. 4 Опыты полного двухфакторного эксперимента.

Как видно из рис. 4, опыты, приведенные в табл. 4, соответствуют на факторной плоскости вершинам квадрата с центром в начале координат.

В табл. 5 приведены условия опытов полного трехфакторного эксперимента. Эти опыты соответствуют в факторном пространстве вершинам куба с центром в начале координат.

Таблица 5.

Полный трехфакторный эксперимент.

Номер опыта	Факторы	Функция отклика
x 1	x 2	x 3
	-1	-1	-1	y1
	+1	-1	-1	y2
	-1	+1	-1	y3
	+1	+1	-1	y4
	-1	-1	+1	y5
	+1	-1	+1	y6
	-1	+1	+1	y7
	+1	+1	+1	y8

Из табл. 4 и 5 видны основные принципы построения матриц планирования полного факторного эксперимента:

уровни варьируемого первого фактора чередуются от опыта к опыту;

частота смены уровней варьирования каждого последующего фактора вдвое меньше, чем у предыдущего.

Матрица планирования полного факторного эксперимента обладает следующими свойствами:

(6.4)

(6.5)

(где l ≠m) (6.6)

Здесь N – число опытов полного факторного эксперимента;

l – номер опыта;

i, l, m – номера факторов.

Свойство выраженное равнением (6.6.), называется ортогональностью. Поэтому говорят, что матрица полного факторного эксперимента ортогональна. Это свойство позволяет вычислять коэффициенты регрессии по простым формулам не зависимо друг от друга.

Общее количество опытов в матрице планирования

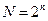(6.7)

где n – число факторов.

На основании полного факторного эксперимента вычисляют коэффициенты регрессии, пользуясь следующими формулами:

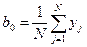(6.8)

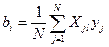(6.9)

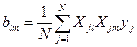(где l ≠m) (6.10)

Некоторые из коэффициентов регрессии могут оказаться пренебрежимо малыми – незначимыми. Чтобы установить, значим коэффициент или нет, необходимо, прежде всего, вычислить оценку дисперсии, с которой он определяется:

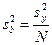(6.11)

Следует отметить, что с помощью полного факторного эксперимента все коэффициенты определяются с одинаковой погрешностью. Принято считать, что коэффициент регрессии значим, если выполнено условие

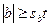(6.12)

где t – значение критерия Стьюдента^*(см. Приложение 3).

В противном случае коэффициент регрессии незначим, и соответствующий член можно исключить из уравнения.

Получив уравнение регрессии, следует проверить его адекватность, т.е. способность достаточно хорошо описывать поверхность отклика. Эту проверку осуществляют с помощью критерия Фишера, который представляет собой следующие отношение:

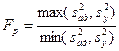(6.13)

где – оценка дисперсии адекватности.

В числителе дроби (2.13) находится большая, а в знаменателе – меньшая из указанных оценок дисперсий.

Оценку дисперсии адекватности вычисляют по формуле

(6.14)

где В – число коэффициентов регрессии искомого уравнения, включая и свободный член;

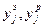– экспериментальное и расчетное значение функции отклика в j -м опыте;

N – число опытов полного факторного эксперимента.

С оценкой дисперсии адекватности связано число степеней свободы

(6.15)

Уравнение регрессии считается адекватным, если выполняется условие

F_p≤F (6.16)

где F – значение критерия Фишера (из Приложения 4).

Для пользования Приложением 4 не обходимо знать число степеней свободы, связанных с числителем и знаменателем выражения (6.13)

Пример 6.1. Рассмотрим химический процесс, в котором выход продукта реакции y (%) зависит от температуры реакционной смеси x ₁ (°C) и концентрации реагента x ₂ (%). Требуется с помощью полного факторного эксперимента найти математическое описание этого процесса в окрестн6ости точки факторного пространства с координатами x ₀₁=50°С и x ₀₂=25%.

Решение. Математическое описание рассматриваемого процесса будем искать в виде уравнения регрессии

где кодирование переменные связаны с температурой и концентрацией следующими соотношениями:

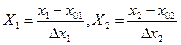
при проведении полного факторного эксперимента зададимся условиями, приведенными в таблице 6.

Таблица 6.

Основные характеристики плана экспериментов

Характеристика……	x 1 °C	x 2 %.
Интервал варьирования…..
Основной уровень…..
Верхний уровень…..
Нижний уровень

Матрица планирования и результаты полного факторного эксперимента представлены в таблице 7.

Таблица 7.

Полный двухфакторный эксперимент

Номер опыта	x 1	x 2	x 1 °C	x 2 %	%
	-1	-1			35,5
	+1	-1			38,5
	-1	+1			32,6
	+1	+1			36,2

На основании результатов полного факторного эксперимента рассчитаем коэффициенты регрессии, пользуясь формулами (6.8) и (6.9):

Примем, что с этой величиной связаны 3 степени свободы.

Ошибку в определении коэффициентов регрессии вычислим по формуле

Пользуясь Приложением 3, находим, что для доверительной вероятности Р=0,95 и 3 степеней свободы значения критерия Стьюдента t=3,18.

Тогда

Для оценки значимости коэффициентов регрессии рассмотрим следующие соотношения:

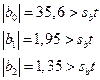
Отсюда видно, что все коэффициенты регрессии значимы. Следовательно, искомое уравнение имеет вид:

y =35,6+1,95X₁-1,35X₂

Для проверки адекватности уравнения регрессии найдем расчеты значения функции отклика:

По формуле (6.14) вычислим оценку дисперсии адекватности:

=

С ней связано число степеней свободы

Рассчитаем значение критерия Фишера, находим по формуле:

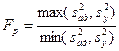
Оно не превосходит значения, приведенного в Приложении 4. Следовательно, уравнение регрессии адекватно.

6.3 Метод дробных реплик

С увеличением количества факторов резко возрастает количе­ство опытов" полного факторного эксперимента. Это видно из урав­нения (6.7). Однако для нахождения коэффициентов регрессии не всегда требуется много опытов. В таких случаях можно уменьшить объем экспериментальных работ, воспользовавшись методом дробных реплик.

Рассматриваемый метод заключается в том, что для нахожде­ния математического описания процесса используется определен­ная часть полного факторного эксперимента: 1/2, 1/4 и т. д. Эти системы опытов называются дробными репликами (см. табл. 8).

Таблица 8.

Полный трехфакторный эксперимент и его дробные реплики

Номер опыта	Факторы	Функция отклика	Дробные реплики
x 1	x 2	x 3
	-1	-1	-1	y1	1/2
	+1	-1	-1	y2
	-1	+1	-1	y3
	+1	+1	-1	y4
	-1	-1	+1	y5	1/2
	+1	-1	+1	y6
	-1	+1	+1	y7
	+1	+1	+1	y8

Расчет коэффициентов регрессии, проверка значимости коэф­фициентов и адекватности математического описания в данном случае производятся так же, как и при полном факторном экспе­рименте.

Пусть, например, требуется найти коэффициенты уравнения регрессии

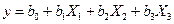Если для этой цели воспользоваться полным трехфакторным экспериментом, то необходимо провести 8 опытов. Однако эту задачу можно решить и с помощью меньшего количества опытов. Например, возьмем матрицу полного двухфакторного эксперимента (табл. 9) и приравняем произведение Х₁ Х₂ к фактору Х₃.

Пользуясь формулой (6.8), вычислим:

С помощью формулы (6.9) найдем:

Таблица 9.

Планирования типа 2^3-1

Номер опыта	x 1	x 2	x 1 x 2	x 3	Функция отклика
	-1	-1	+1	+1	y1
	+1	-1	-1	-1	y2
	-1	+1	-1	-1	y3
	+1	+1	+1	+1	y4

Отметим, что в табл. 9 столбцы для произведения Х₁Х₂ и фак­тора Х₃ полностью совпадают. Поэтому коэффициенты b₁₂ и b₃ не могут быть определены раздельно. С помощью формулы (6.9) может быть найдена только их сумма:

Этот недостаток рассматриваемого плана является своеобраз­ной «платой» за уменьшение общего количества опытов с восьми до четырех,

Такое планирование эксперимента, когда некоторые из факто­ров приравнивают к произведениям нескольких факторов, назы­вается планированием со смешиванием. Его обозначают символом 2^n-p где п — общее число факторов, а р — число факторов, при­равненных к произведениям. С этой точки зрения в табл. 9 при­ведена матрица планирования типа 2^3-1.

Существует правило, позволяющее определить, какие коэффи­циенты регрессии определяются совместно при планировании со смешиванием. Рассмотрим это правило па конкретном примере.

Пример 6.2. Методом дробных реплик будем искать математи­ческое описание процесса в виде уравнения регрессии:

Воспользуемся планированием типа 2^5-2 и примем:

Такие равенства в методе дробных реплик называются генерирующими соотношениями.

Следует отметить, что выбор генерирующих соотношений в общем случае произволен. Однако он существенно влияет на характер совместных оценок коэффициентов регрессии.

Правило определения совместных оценок коэффициентов состоит в следующем:

1. Примем во внимание, что

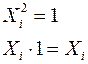
2. Умножив обе части генерирующих соотношений соответственно на Х₄ и Х₅, получим:

Эти равенства называются определяющими контрастами. Пе­ремножив их почленно, получим новые определяющие контрасты. В данном случае это

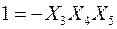
3. Составим алгебраическую сумму из единицы и правых ча­стей всех полученных определяющих контрастов:

4. Умножив каждый из факторов на S и заменив факторы со­ответствующими коэффициентами разложения в ряд Тейлора (6.2), получим:

6.4 Устранение влияния временного дрейфа

Планирование со смешиванием иногда применяют в тех слу­чаях, когда необходимо устранить влияние неуправляемых вре­менных изменении некоторых влияющих факторов, называемое временным дрейфом.

Дело в том, что при постановке большой серии опытов, требую­щих длительного времени, всегда приходится опасаться нежела­тельных изменений исходных свойств реагентов, катализаторов, некоторых характеристик оборудования и т. п. Влияние этого вре­менного дрейфа на параметры математического описания процесса можно практически устранить, разбивая серию опытов на отдель­ные блоки так, чтобы эффект от временного дрейфа оказался смешанным с произведениями факторов, для которых коэффи­циенты регрессии достаточно малы.

Допустим необходимо устранить влияние временного дрейфа на параметры уравнения регрессии, получаемого в результате пол­ного трехфакторного эксперимента. С этой целью разобьем экспе­римент на дна блока и введем новую независимую переменную Х _д характеризующую дрейф. Положим Х _д = X₁X₂X_3.

В один из блоков отберем опыты, для которых Х _д = +1, а в другой —для которых Х _д= -1. Формально это планирование, приведенное в табл. 10, можно рассматривать как эксперимент типа 2^4-1 с генерирующим соотношением Х _д = Х₁Х₂Х₃.

Таблица 10.

Планирование в условиях временного дрейфа

Номер блока	Х 1	Х 2	Х 3	Х д= Х1Х2Х3	Функция отклика
	–1	–1	+1	+1	у 1+βд
+1	–1	–1	+1	у 2+βд
–1	+1	–1	+1	у 3+βд
+1	+1	+1	+1	у 4+βд
	–1	–1	–1	–1	у 5 –βд
+1	–1	+1	–1	у 6 –βд
–1	+1	+1	–1	у 7 –βд
+1	+1	–1	–1	у 8 –βд

Исходя из матрицы планирования, будем считать, что в первом блоке все результаты опытов вследствие временного дрейфа завышены на β_д, а во втором – занижены на эту величину.

Если уравнение регрессии ищется в виде

то коэффициенты регрессии будут являться следующими оценками:

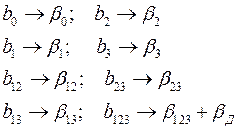
Рассчитаем, например, коэффициенты b₁ и b₁₂₃:

Следовательно, все коэффициенты регрессии, кроме b₁₂₃, не содержат погрешностей, обусловленных временным дрейфом.

Дата добавления: 2014-01-20