Оптимизация

7.1 Метод крутого восхождения

Здесь мы рассмотрим вопрос о том, как использовать эти модели для оптимизации процессов или свойств многокомпонентных систем.

Следует иметь в виду, что качество процесса обычно характе­ризуется несколькими функциями отклика. Однако обычно невоз­можно найти такое сочетание значении влияющих факторов, при котором одновременно достигаются эксперименты всех интересующих экспериментатора функции отклика. Например, максимальная производительность оборудования и минимальная себестоимость продукции обычно достигаются при различных технологических ре­жимах.

Важно отметить, что как влияющие факторы, так и функции отклика могут изменяться только в определенных пределах. Так, концентрации реагентов не могут быть отрицательными, температура и давление в аппарате не могут превышать безопасных пре­делов, себестоимость продукции должна быть не выше плановой и

т. п. Следовательно, оптимизацию процессов, как правило, осу­ществляют в условиях ограничений на влияющие факторы и функ­ции отклика.

Величина, характеризующая уровень оптимизации процесса, называется критерием оптимальности. В частном случае крите­рием оптимальности может быть одна или функции отклика, характеризующих процесс.

Оптимизация процесса представляет coбой целенаправленный поиск значений влияющих факторов, при которых достигается экстремум критерия оптимальности (с учетом ограничений, нало­женных на все влияющие факторы и функции отклика).

Д. Бокс и К. Уилсон предложили использовать для опти­мизации результаты полного факторного эксперимента или эксперимента по методу дробных реплик. Сущность такой оптимизации состоит в следующем.

Пусть, например критерием оптимальности служит функция отклика у, представленная в виде (6.3).

Один из влияющих факторов принимают за базовый и для него вычисляют произведение соответствующего коэффициента регрес­сии на шаг варьирования. Например, для мерного фактора это произведение имеет вид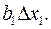

Затем дли базового фактора выбирают шаг движения , с которым будет осуществляться оптимизация. Обычно .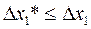

После этого вычисляем соотношение:

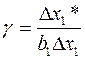(7.1)

Для всех остальных факторов шаги движения к оптимальным значениям рассчитывают по формуле:

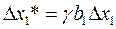(7.2)

Движение к оптимуму начинают из центра плана, который использовался для получения математического описания функции отклика. Значения факторов на каждом новом шаге нахо­дят путем прибавления к соответствующим предыдущим значениям. Так осуществляет­ся оптимизация по методу кру­того восхождения.

Если же ищется минимум функции у, то новые значения факторов находят из преды­дущих, путем вычитания . Такой способ оптимизации на­зывают методом наискорей­шего списка.

Рис 5. Оптимизация по методу кругового восхождения.

Движение к оптимуму пре­кращают в следующих слу­чаях:

1. Значения (одного или нескольких) факторов или функций отклика вышли на границы допустимых значений.

2, Достигнут экстремум критерия оптимальности у.

В первом случае на этом оптимизация заканчивается, а во вто­ром – в области экстремума функции у ищут ее новое математи­ческое описание, используя полный факторный эксперимент или метод дробных реплик. Если удается получить адекватное описа­ние этой функции в виде (6.3), то продолжают оптимизацию ме­тодом крутого восхождения (рис. 5). Очевидно, оптимум, найдем в результате первого крутого восхождения, был локальным.

Если же в области оптимума не удается получить адекватного уравнения регрессии вида (6.2),то переходят к планированию эксперимента для получения математического описания функции у в виде многочлена второй степени.

Пример 7.1. Пусть в результате полного факторного экспери­мента (пример 6.1) получено адекватное уравнение регрессии

y₁ =35,6+1,95 X ₁-1,35 X ₂

Здесь, как и в примере 6.1, y₁ — выход продукта реакции, X ₁ — температура,

X 2 – концентрация реагента.

Введем также в рассмотрение функцию отклика y₂, характеризующую скорость химической реакции (кмоль ×м^-3∙ч^-1). Пусть требуется, чтобы выполнялось условие у ₂ ³ 2,5.

Допустим, что ограничения на влияющие факторы имеют вид

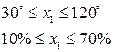
Будем оптимизировать выход продукта реакции методом кру­того восхождения.

В качестве базового фактора возьмем температуру и примем шаг движения на крутом восхождении 4°, тогда

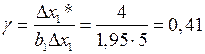
Здесь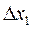взят по условиям полного факторного эксперимента (пример 6.1).

Шаг по концентрации на крутом восхождении равен

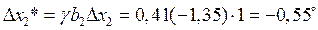
Для удобства ведения эксперимента шаги движения, рассчитан­ные по формуле (7.2), можно несколько округлять. В данном слу­чае удобно принять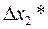— 0,5°.

Результаты опытов, выполненных по методу крутого восхожде­ния, приведены в табл. 11. Здесь у ₁^р и у ₁^э— соответственно рас­четные и экспериментальные значения выхода продукта реакции, у ₂^э — экспериментально найденные скорости реакции.

Шаги движения в координаты опытов крутого восхождения в колированных переменных рассчитываются по формуле (6.1) с использованием физических переменных х ₁, х ₂ и шагов варьирования, принятых ранее в полном факторном эксперименте.

Как видно из табл. 11, в опыте № 4 – достигнут максимальный выход продукта реакции, однако скорость процесса в этом случае меньшие допустимого значения. По-видимому, оптимальным режи­мом процесса следует считать условия опыта № 3.

Ограничения на х ₁ и х ₂ в ходе оптимизации не нарушены.

Таблица 11.

Результаты опытов по методу крутого восхождения

Характеристика и номер опыта	х 1	х 2	Х 1	Х 2	у 1^р	у 1^э	у 2^э
Центр плана					35,6	35,1	2,9
Интервал варьирования					-	-	-
Шаг движения		-0,5	0,8	-0,5	-	-	-
Крутое восхождение
Опыт №1		24,5	0,8	-0,5	36,5	36,9	3,2
№2		24,0	1,6	-1,0	37,4	37,2	3,7
№3		23,5	2,4	-1,5	38,2	38,5	2,8
№4		23,0	3,2	-2,0	39,1	40,1	2,3
№5		22,5	4,0	-2,5	40,0	38,1	1,9
№6		22,0	4,8	-3,0	40,9	37,2	1,6

7.2 Симплексный метод

Симплексом называется правильный многогранник, имеющий n+ 1 вершину, где п — число факторов, влияющих на процесс. Так, если факторов два, то симплексом является правильный тре­угольник. Сущность симплексного метода оптимизации иллюстрирует рис. 6.

Рис. 6. Оптимизация по симплексному методу.

Начальная серия опытов соответствует вершинам исходного симплекса (точки 1, 2 и 3).Условия этих первых опытов берутся из области зна­чении факторов, соответствую­щих наиболее благоприятным из известных режимов оптими­зируемого процесса.

Сравнивая между собой результаты опытов в точках 1, 2 и 3, находят среди них самый «плохой», с точки зрения выбранного критерия опти­мальности. Пусть, например, самым «неудачным» оказался опыт в точке 1. Этот опыт исключают из рассмотрения, а вместо него в состав симплекса вводят опыт в точке 4, которая симметрична точке 1 относительно противоположной стороны треугольника, со­единяющей точки 2 и 3.

Далее сравнивают между собой результаты опытов в верши­нах нового симплекса, отбрасывают самый «неудачный» из них и переносят соответствующую вершину комплекса в точку 5. Затем рассмотренная процедура повторяется в течение всего процесса оптимизации.

Если достигнут экстремум критерия оптимальности, то даль­нейшее движение симплекса прекращается. Эго значит, что новый шаг возвращает исследователя, а предыдущую точку факторного пространства.

Следует иметь в виду, что симплексный метод, так же как и метод крутого восхождения, является локальным методом поиска экстремума. Если существует несколько экстремумов контроля оптимальности, то этот метод позволяет найти тот из них который расположен ближе к точкам исходного симплекса. Поэтому, если есть подозрение о существовании нескольких экстремумов критерия оптимальности; то нужно осуществить их поиск, каждый раз начиная оптимизацию из новой области факторного пространства. Затем следует сравнить между собой найденные оптимальные условия и из всех вариантов выбрать наилучший.

При оптимизации необходимо принимать во внимание ограни­чения, наложенные на влияющие факторы и функции отклика.

Важно отметить, что при пользовании симплексным методом не обязательно дублировать опыты. Дело в том, что ошибка в от­дельном опыте может только несколько замедлить оптимизацию. Если же последующие опыты выполняются безупречно, то движе­ние к оптимуму продолжается.

Матрица опытов исходного симплекса в кодированных пере­менных приведена в табл. 12. Символом «0» обозначены коорди­наты центра плана, т. е. основной уровень.

Таблица 12.

Матрица исходного симплекса

Номер опыта	Х 1	Х 1	…	Х n-1	Х n	Функция отклика
	k1	k2	…	kn-1	kn	у 1
		k2	…	kn-1	kn	у 2
		-R2	…	kn-1	kn	у 3
…	…	…	…	…	…	…
n-1			…	kn-1	kn	у n-1
n			…	-R n-1	kn	у n
n+1			…		-R n	у n+1

Величины входящие в эту таблицу, рассчитываются по следующим формулам:

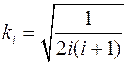(7.3)

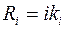(7.4)

Здесь i – номер фактора в матрице планирования.

Опыты представленные в табл.12, соответствуют вершинам симплекса, сторона которого равна единице, а центр совпадает с началом координат (в координатных переменных).

Результаты расчетов, выполненных на основании табл. 12 и формул (7.3) и (7.4), приведены в табл. 13.

Таблица 13.

Условия начальной серии опытов

Номер опыта	Х 1	Х 2	Х 3	Х 4
	0,5	0,289	0,204	0,158
	-0,5	0,289	0,204	0,158
		-0,587	0,204	0,158
			-0,612	0,158
				-0,632

Аналогично можно рассчитать условия исходной серии опытов для большего количества факторов.

Очевидно, наибольшее количество опытов приходится ставить в начале эксперимента. Затем на каждом шаге оптимизации вы­полняется только один опыт.

Приступая к оптимизации, необходимо с помощью табл. 12 или 13 рассчитать матрицу исходной серии опытов в физических пе­ременных, пользуясь формулой

(7.5)

где использованы те же обозначения, что и в формуле (6.1). В дальнейшем все операции производятся только с физическими переменными.

Условия каждого нового опыта рассчитываются по формуле

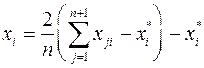(7.6)

где n – число факторов в матрице планирования;

j – номер опыта;

i – номер фактора;

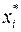– значение i- го фактора в самом «неудачном» опыте предыдущего симплекса.

Следует отметить, что на любом шаге, оптимизации, осуществ­ляемой симплексным методом, можно включить в программу ис­следований новый фактор, который до тех пор не принимался во внимание, но оставался на постоянном уровне. При этом значения всех ранее рассматриваемых факторов рассчитываются по фор­муле

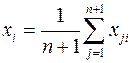(7.7)

где i = 1, 2,..., п, т. е. являются средними арифметическими зна­чениями соответствующих координат предыдущего симплекса.

Значение вновь вводимого фактора определяется по формуле

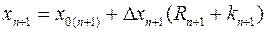(7.7)

где х_0(n+1) — основной уровень фактора;

Δх_0(n+1) — выбранный шаг варьирования для данного фактора;

R_n+1, k_n+1— величины, рассчитываемые по формулам (7.3) и (7.4). Отметим, что добавление нового фактора в состав полного фак­торного эксперимента сопровождается увеличением количества опытов вдвое. В этом смысле симплексный метод имеет очевидное преимущество.

В практику научных исследований симплексный метод был вве­ден Ф, Химевортом в 1962г.

Пример 7.2. Пусть требуется с помощью симплексного метода оптимизировать выход целевого продукта у (%), который полу­чается при взаимодействии двух реагентов с концентрациями х ₁и х ₂ (кмоль∙м^-3) при температуре х ₃ (°С).

Выберем основные уровни и шаги варьирования факторов и сведем их в табл. 14.

Таблица 14.

Значения уровнейфакторов и шагов варьирования

Фактор	Основной уровень	Шаг варьирования
х 1 кмоль∙м^-3	1,0	0,1
х 2 кмоль∙м^-3	1,5	0,2
х 3 °С	60,0	5,0

Пользуясь формулой (7.5) и табл. 13, рассчитаем условия про­ведения первых четырех опытов и полученные результаты сведем в табл. 15. Так, для третьего опыта

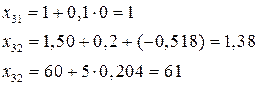
Здесь первый индекс обозначает номер опыта, а второй — номер фактора.

Сравнивая между собой результаты первых четырех опытов, видим, что самый низкий выход целевого продукта получился в третьем опыте. Этот опыт следует исключить из дальнейшего рассмотрения,

Заменим его опытом № 5, условия проведения которого рассчи­таем по формуле (7.6):

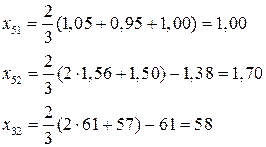
Таблица 15.

Условия и результаты планирования по симплексному методу

Номер опыта	х 1	х 2	х 3	Функция отклика
	1,05	1,56		72,3
	0,95	1,56		70,1
	1,00	1,38		65,4
	1,00	1,50		68,2
	1,00	1,70		73,9
	1,00	1,72		76,5

В новом симплексе, образованном опытами № 1, 2, 4 и 5, самым «неудачным» является опыт № 4. Его заменим опытом № 6, усло­вия которого найдем, пользуясь той же формулой (7.6).

Далее процедура оптимизации может быть продолжена ана­логично.

Рассмотрим теперь вопрос о том, как включить в программу исследований еще одни фактор, например, скорость- вращении мешалки. Пусть до этих пор она была постоянной и равной 500 об/мин. Теперь будем считать эту величину фактором х ₄ и примем для нее шаг варьирования Δх₄ = 100 об/мин.

Предыдущий симплекс для трех факторов (см. табл. 15) со­стоит из опытов № 1, 2, 5 и 6. Чтобы из него получить новый сим­плекс для четырех факторов, введем опыт № 7 (табл. 16).

Таблица 15.

Симплексный план эксперимента для четырех факторов

Номер опыта	х 1	х 2	х 3	х 4	Функция отклика
	1,05	1,56			72,3
	0,95	1,56			70,1
	1,00	1,70			73,9
	1,00	1,72			76,5
	1,00	1,64			78,1

Условия проведения опыта № 7 найдем по формулам (7.7) и (7.8):

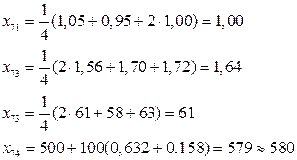
Далее оптимизацию можно продолжить с учетом всех четырех факторов, пользуясь рассмотренной выше процедурой.

Дата добавления: 2014-01-20