Расстановка ключей

Хеширование

Таблицы

Таблица – это структура данных, в которой каждому элементу соответствует определенное имя.

Каждый элемент таблицы обычно представляется записью, которая содержит ряд информационных полей. Одно или несколько полей играют особую роль и используются при поиске элемента. Их называют ключами записи. Ключ – обычно целое положительное число. Элементы добавляются в таблицу и выбираются из таблицы по ключам.

Операции над таблицами:

1. поиск записи с заданным ключом,

2. включение в таблицу записи с заданным ключом (если есть запись с заданным ключом в таблице, то это означает замену старой записи на новую),

3. исключение записи с заданным ключом.

Хешированием называется процесс выделения элемента индексного массива непосредственно по информации, которая содержится в массиве.

Идея хеш-реализации состоит в сведении работы с одним большим множеством к работе с массивом небольших множеств.

Для построения хеш-таблицы (перемешанной или рандомизированной) с N входами выбирается функция отображения, преобразующая ключ К в число k из диапазона от 0 до N-1.

Идеальная функция отображения преобразовала бы все встречающиеся ключи в различные числа.

Элемент с ключом К помещается в К-ую позицию таблицы.

Для поиска элемента применяется та же функция отображения и ищется К-ый элемент таблицы.

Если таблица содержит М элементов, ее размер выбирается равным

N=1,5*М.

Такое решение дает разумный компромисс между размером таблицы и средней длиной поиска.

Функция отображения М(К) выбирается так, чтобы любое число из диапазона от 0 до N-1вырабатывалась бы с приблизительно равной вероятностью для заданного или же возможного набора ключей.

Простой способ достижения этой цели заключается в том, что в качестве значения хеш-функции берется остаток от деления на N значения ключа, рассматриваемое как двоичное число.

При заполнении таблицы возникают коллизии – ситуации, когда для двух неодинаковых ключей функция вычисляет один и тот же адрес.

	Методы разрешения коллизий

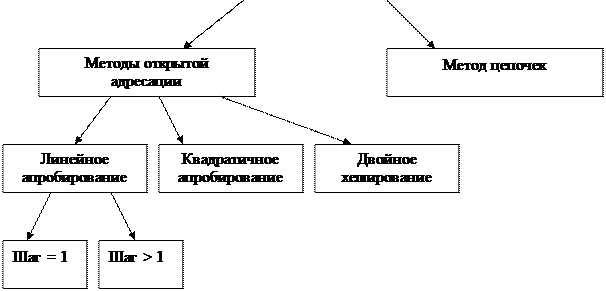
Рис. 20. Методы разрешения коллизий

Рассмотрим линейное апробирование с шагом 1.

Линейное апробирование сводится к последовательному перебору элементов таблицы с некоторым фиксированным шагом. Рассмотрим метод на примере гипотетического ассемблера.

Пусть:

1. имена идентификаторов состоят из двух знаков, первый – буква, второй – десятичная цифра;

2. количество идентификаторов равно 7: А3, В5, С1, С4, D4, D9, X3; следовательно, хеш-таблица имеет 1,5*7=10 входов;

3. позицию ключа в таблице дает функция отображения

K=K_d=M(K), где K_d – десятичная цифра идентификатора.

Вход	1 шаг	2 шаг	3 шаг	4 шаг	5 шаг	6 шаг	7 шаг	Длина поиска
				С1	С1	С1	С1
	А3	А3	А3	А3	А3	А3	А3
			X3	X3	X3	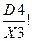X3	X3
		В5	В5	В5	В5	В5	В5
					С4	С4	С4
							D4
						D9	D9
Средняя длина поиска равна	1,86

При линейном поиске необходимы были бы в среднем 4 пробы, а при двоичном – 2,9 пробы.

Анализ линейного апробирования:

Е = (1- а /2) / (1- а)

Дата добавления: 2014-01-20