Сбалансированные деревья

End

Begin

Then

Begin

End

Begin

Then

Else

Then

Else

Then

Else

End

Begin

Begin

Else

Then

Else

Then

Begin

End

Else

Then

Else

Then

Begin

Else

Then

Else

Then

Else

Then

Begin

End

Begin

Else

Then

Begin

Then

Else

Then

Else

Then

Begin

Then

Else

Then

Else

End

Begin

Begin

Begin

Else

Then

Begin

Действия над бинарными деревьями

Описание бинарного дерева

type refnode=^node {refnode - ссылка}

node= record {node - узел}

inf: integer;

left: refnode; {ссылка на левое поддерево}

right: refnode; {ссылка на правое поддерево}

end;

- просмотр:

{прямой просмотр дерева}   procedure Browser1 (root: refnode); begin if root <> nil then begin write(root^.inf); Browser1 (root^.left); Browser1 (root^.right) end end;

{обратный просмотр дерева}   procedure Browser2 (root: refnode); begin ifroot <> nil then begin Browser2 (root^.leIt); Write(root^.inf); Browser2 (root^.right) end end;

{концевой просмотр дерева}   procedure Browser3 (root: refnode); begin if root <> nil then begin BrowserЗ (root^.left); BrowserЗ (root^.right); write(root^.inf) end end;

- подсчет количества вершин:

function Counter (root: refnode): integer;

if root = nil

Counter:= 0

Counter:= 1 + Counter(root^.left) + Counter(root^.right)

end;

- включение данных в дерево:

procedure Include (var root: refnode; x: integer);

if root = nil then

new (root);

with root^ do

left:= nil;

right:= nil;

inf:= x

end;

with root^do

if x < inf

Include(left, x)

if x> inf

Include(right, x)

else {ничего не делаем, т.к. значение х

уже есть}

end;

- поиск данных:

{отыскание вершины со значением х в дереве с корнем root}

function Find (root: refnode; x: integer): refnode;

if root = nil

Find:= nil

with root^ do

if x< inf

Find:= Find(left, x)

if x> inf

Find:= Find(right, x)

else Find:= root

end;

- удаление вершин из дерева:

procedure Delete (var root: refnode; x: integer);

var q: refnode;

procedure del (var r: refnode);

if r^.right <> nil

del(r^.right)

q^.inf:= r^.inf;

q:=r;

r:= r^.left

end; {procedure del}

if root = nil

write (‘такой вершины нет в дереве’)

if x < root^.inf

Delete(root^.left, x)

if x > root^.inf

Delete(root^.right, x)

{удаляем вершину, на которую указывает root}

q:= root;

if q^.right = nil

root:= q^.left

if q^.left = nil

root:= q^. right

del(q^.left);

dispose (q)

end; {procedure Delete}

- сравнение деревьев:

function Equal(root 1, root2: refnode): Boolean;

if root 1 <> nil and root2 <> nil

Equal:= (rootl^.inf = root2^.inf) and

Equal(rootl^.left,root2^.left) and

Equal(root1^.right, root2^.right)

if (root1 = nil) and (root2 = nil)

Equal:= true

Equal:= false

end; {function Equal}

- слияние деревьев:

{слияние деревьев переносом вершин второго дерева в первое}

procedure Merger_M(var root1: refnode; root2:. refnode);

var l, r: refnode;

procedure Insert(var root: refnode; elem: refnode);

{включение элемента elem в дерево с корнем root1}

if root = nil {в дереве Т1 найдено вакантное

место для ссылки}

then {то}

{устанавливаем ссылку в дереве Т1

на включаемый элемент дерева Т2 и разрываем

связи элемента с деревом Т2}

root:= elem;

elem^.left:= nil;

elem^.right:= nil;

with root^ do {ищем место для включения

элемента}

if elem^.inf < inf

Insert(left, elem)

if elem^.inf > inf

Insert(right, elem)

dispose (elem) {уничтожаем

элемент, т.к. такое значение уже есть}

end; {procedure Insert}

begin {procedure Merger_M}

if root2 <> nil

l:= root2^.left; {сохраним ссылку на левое

поддерево}

r:= root2^.right; {сохраним ссылку на правое

поддерево}

Insert(root1,root2); {отдали вершину root2 в

дерево Т1}

Merger_M(root1,l); {слияние левого поддерева с

Tl}

Merger_M(root1,r); {слияние правого поддерева с

Tl}

end; {procedure Merger_M}

- уничтожение дерева:

{уничтожение дерева, начиная с корневой вершины}

procedure Destroyl (root: refnode);

var l, r: refnode;

if root <> nil

l:= root^.left; {сохраним ссылку на левое

поддерево}

r:= root^.right; {сохраним ссылку на правое

поддерево}

dispose (root);

Destroyl (l); {уничтожим левое поддерево}

Destroyl (r); {уничтожим правое поддерево}

end;

Примеры использования деревьев:

- дерево двоичного поиска,

- дерево частотного словаря,

- дерево синтаксического анализа.

Дерево частотного словаря – результат построения дерева двоичного поиска для слов некоторого текста.

Генерирование дерева частотного словаря полезно при подсчете количества вхождений каждого слова в некоторый текст.

Описание дерева частотного словаря:

type ukazatel=^tree;

derevo= record

slovo: string[20];

kolichestvo: integer;

left: ukazatel;

right: ukazatel;

end;

Дерево синтаксического анализа арифметического выражения – бинарное дерево, листьями которого служат операнды, а остальными вершинами - операции, причем уровень вершины соответствует приоритету выполнения операции: чем ближе к листьям, тем приоритет выше.

Бинарное дерево не является деревом, если оно пустое.

21 апреля

Дерево поиска организовано так, что для каждого узла все ключи (то, что стоит в узле) в левом поддереве меньше значения ключа в предке, а в правом – больше. В таком дереве из n элементов для поиска требуется log₂n сравнений, при этом дерево должно быть сбалансированным.

Идеально сбалансированное дерево – дерево, у которого левое и правое поддерево имеют одинаковую высоту.

Сбалансированным является дерево, у которого разность высот поддеревьев равна единице.

4, 2, 1, 3, 6, 5, 7

Рис. 14. Идеально сбалансированное дерево. Высота равна 2

1, 2, 3, 4, 5, 6, 7

Рис. 15. Список. Высота равна 6

50, 70, 48, 46, 49, 68, 73, 54, 60

Рис. 16. Несбалансированное дерево

Рис. 17. Сбалансированное дерево

14.6. АВЛ – дерево

АВЛ – Адельсон-Вельский[6], Ландис[7].

Балансировка – «борьба» за малую высоту.

Виды балансировки:

1. малая левая,

2. малая правая,

3. большая левая,

4. большая правая.

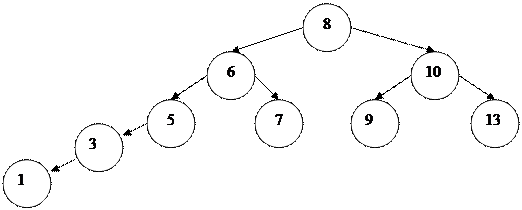Рис. 18. Несбалансированное дерево

После малой левой балансировки:

Рис. 19. Сбалансированное дерево

28 апреля

Дата добавления: 2014-01-20