По способу равных допусков

Примеры решения задач размерных цепей различными методами

Задание:

Для узла на первом рисунке провести сравнительный расчет размерной цепи различными методами.

Рисунок 1. Узел 1.

Выделим размерную цепь из узла:

Рисунок 2. РЦ-А

Всего размеров в размерной цепи n = 7, n = m + p,

где: m -увеличивающих, p-уменьшающих

Увеличивающие размеры А₄, А₅, А_6, уменьшающие размеры А₁, А_2, А₃

Применим формулы:

TA_i=TA_D/ (n-1), TA_i=300мкм/ (n-1) =50мкм

Воспользуемся уравнением:

= –

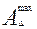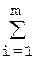
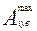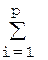
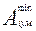
Выбрав в качестве увязочного размера, примем уменьшающий 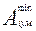, получим:

= – –

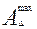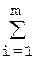
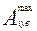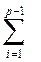
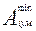Представим графически положение допусков, приняв их в тело детали для всех размеров, кроме увязочного:

Рисунок 3. Поля-А

Найдем его наименьшее значение :

=26,850

Рисунок 4. РЦ-А с отклонениями

В сборке допуски графически можно представить в виде:

Рисунок 5. Графическая цепочка полей допусков А

Представим детали узла 1 с номинальными размерами и допусками, подготовленными к сборке. Получим в графической цепочке, как и было, заказано: S_max=400мкм и S_min=100мкм.

Втулка Шестерня Втулка

Рисунок 6. Составляющие детали узла с допусками размеров и цепочка их расположения

Решение задачи по методу допусков одного квалитета-полной взаимозамеряемости (МПВ).

Решим ту же задачу, но по зависимостям метода полной взаимозаменяемости, не находя допуски по зависимости способа одного квалитета. При определении допуска, для размерной цепи «А» воспользуемся формулой для расчета допуска через коэффициент точности «а»:

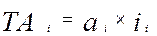
Необходимо определить а и i:

Полагая, что точность изготовления всех деталей одного уровня, можно считать все коэффициенты точности одинаковыми равными а_ср. Этот коэффициент можно получить:

Если же есть детали с заданными допусками, то формула принимает вид:

-допуски готовых деталей, например полученных по кооперации. У нас заданных допусков нет, поэтому вторая сумма в числителе равна нулю. Допуск замыкающего размера будет:

Теперь допуски размеров будут:

что соответствует результату, ранее полученному по способу равных допусков.

В общем случае метод допусков одного квалитета предполагает наличие различных размеров звеньев. Для ранее рассмотренной задачи будем считать, что корпус целиковый и внутренний его размер 81мм.

Для узла 2 выделим размерную цепь обозначив её «В»:

Рисунок 7. Узел 2.

Теперь размерная цепь примет вид:

Рисунок 8. РЦ-В

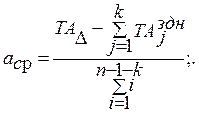
Размеровс заданными допусками нет, поэтому:

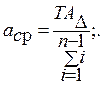
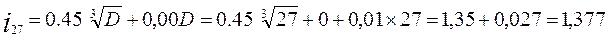
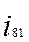
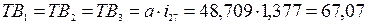
Проверим сумму допусков:

67,07+67,07+67,07+98,781=201,444+98,549=299,871

Округлим допуски до 67 и 99мкм, получим:

67+67+67+99=300

Примем допуски размеров B₁, B₂, B₃ в тело допуска, а B₄ как увязочный размер:

Рисунок 9. Поля-В

Воспользовавшись уравнением для максимального значения замыкающего размера, получим:

,

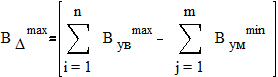
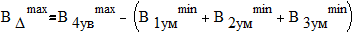
Рисунок 10. РЦ-В с отклонениями размеров

Теперь, представив, полученный результат графически и проверим полученные величины замыкающего размера:

Рисунок 11. Графическая цепочка полей допусков В

По уравнениям можно тоже провести проверку:

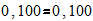
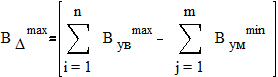
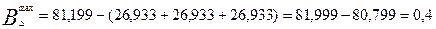
По результатам решения уравнений и графически видно, что задача решена, верно.

Проведём, однако, дополнительно проверку посредством уравнения середины полей допусков:

Здесь обозначено D₀ – середина поля допуска соответствующего размера.

Найдём середины полей известных допусков, за исключением увязочного и обозначим значения на рисунке:

Расположение допусков одинаково, поэтому:

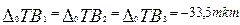
Определим середину поля допуска замыкающего размера:

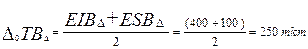
Подставив величины в уравнение, найдём середину поля допуска увязочного размера :

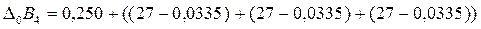
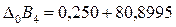
По графической проверке также:

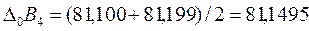
Определим отклонения увязочного размера:

Определим среднюю величину зазора, через допуски по графической цепочке: (100+199)/2+(0+201)/2=149,5+100,5=250мкм

Дата добавления: 2014-01-20