Решение задачи методом компенсации

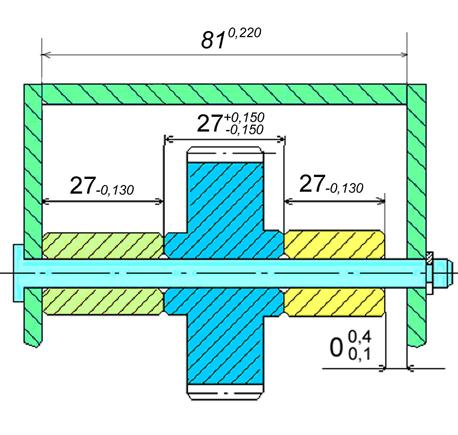
Рисунок 17. УЗЕЛ 3L

Назовем размерную цепь «L»

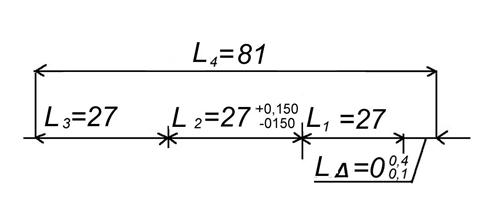
Рисунок 18. ЦЕПЬ L1

Если один из размеров уже имеет отклонения, положим задан размер L_{2 задан} =27±0,150, тогда допуск размера будет 0,3, но и допуск замыкающего тоже 0,3. Подставив значения в зависимость для коэффициента точности получим неопределённость.

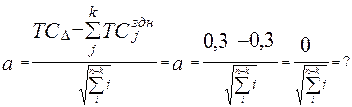
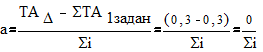
Полученный 0 в числителе не позволяет решить задачу…..

Примем допуски в тело деталей для L₁, L₃, L₄ по 11 квалитету и определим их значения по таблицам стандартов:

TL₁=TL₃=130 TL₄=220

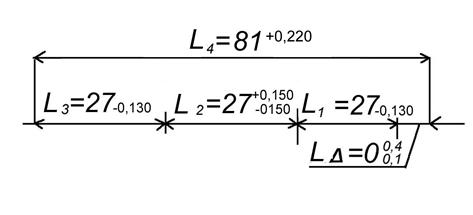
Рисунок 19. ЦЕПЬ L1 с отклонениями размеров

Заметим, что:

L₁,L₃ – охватываемые размеры, поэтому, назначая допуск в тело детали, получим 27_-0,130

L₄ – охватывающий размер, поэтому 81^+0,220

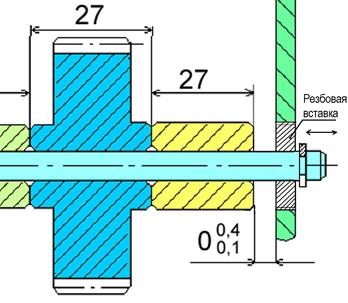
Рисунок 20. Узел с подвижным компенсатором

Для обеспечения плавной компенсации необходимо подготовить соединение с малой осевой подачей (например, при резьбе с шагом Р=0,5 мм предел компенсации будет выбран ~ за 1 оборот). Для обеспечения требуемого замыкающего размера необходимо закрутить компенсирующую пробку до закрытия зазора, а затем отвернуть 1/2 оборота, что обеспечит замыкающий размер 250 мкм, являющийся серединой поля допуска замыкающего размера. Далее необходимо во впадине фиксирующей гайки подготовить резьбовое отверстие и зафиксировать ее винтом М4. В противном случае вибрации могут отпустить соединение и нарушить регулировку.

Как видно, такое решение хотя и удобно, но технологически требует специального узла, громоздкого, хотя и простого в регулировке. В конструкциях часто удобнее применять жесткие компенсаторы, число которых может быть рассчитано.

По МПВ ?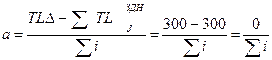

Решать нельзя.

Аналогично ТВМ, L₁ L₂ L₃ назначим по IT 11,

ТА₁ = ТА₃ = 130

ТА₄ = 220

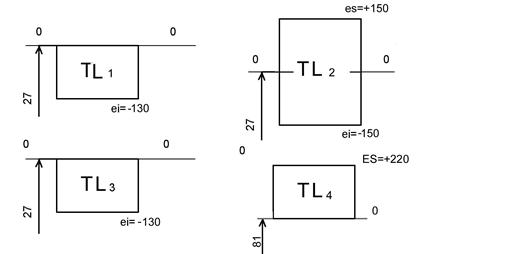
Рисунок 21. ПОЛЯ L

но ТLΔ д.б. равно S ТL_i

Проверим:

300 ¹ 130 + 300 + 130 + 220. 300 ¹ 780

для удовлетворения равенства введём компенсатор и запишем

ТLΔ = S LА_i – ТL_к ® ТL_к = S ТL_i – ТLΔ

ТL_к = 780 –300 = 480

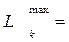(81.0 + 0.220) – ((27.0 – 0.130) + (27.0 – 0.150) + (27.0 – 0.130)) – 0.400

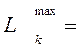81.220 – (26.830 + 26.850 + 26.870) – 0.400

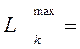0.230

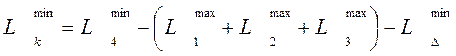
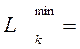81 – (27 + 27.150 + 27) – 0.1

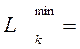81 – (81.150 + 100)

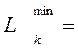- 0.250 отрицательный комплекс?

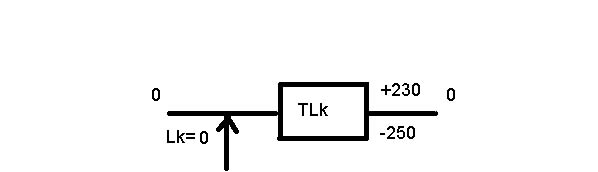
Рисунок 22. Поле компенсации 1

Так, в одном случае прокладок добавлять, в другом – удалять 250 мкм

Полученный вариант решает проблему лишь частично, т.к. -0.250 придется припиливать…, а +230 приводит к выходу за L_D.

Уменьшим размер L₁ на 1 мм, и теперь. L₁ = 26мм.

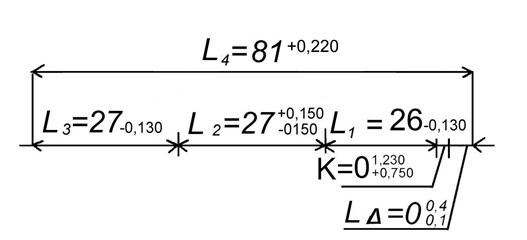
Рисунок 23. Окончательная цепь L

Тогда:

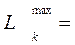81.220 – (26.830 + 26.850 + 25.870) – 0.400

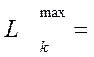81.220 – 79.990 = 1.23 мм

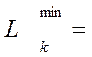81 – (27 + 27.150 + 26) – 0.1

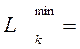0.750

ТL_к = 1.23 – 0.750 = 0.480 мм

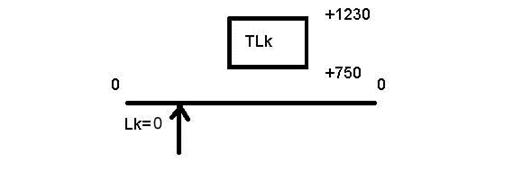
Рисунок 24. Поле компенсации 2

Толщина первой постоянной прокладки соответствует минимальной компенсации S1=0,750мм.

Число ступеней компенсации

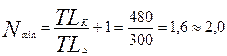
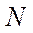при необходимости, должно округлять в большую сторону.

Теперь определим толщину компенсационных прокладок, если известно их число и они должны при их применении укладываться в пределах замыкающего размера:

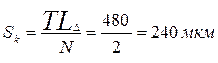
есть по R20, но лучше по R 10 принять S=0.25мм,

тогда N

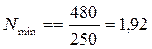
с округлением в большую сторону будет 2.

Теперь ясно, что компенсатор состоит из одной постоянной прокладки 0,750мм и двух сменных 0,250мм.

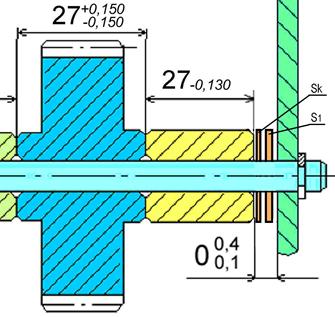
При компенсации будем получать размеры:

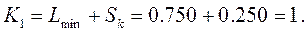
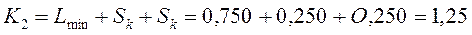
Проверим соответствие неравенству:

=

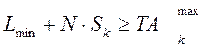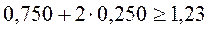
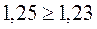
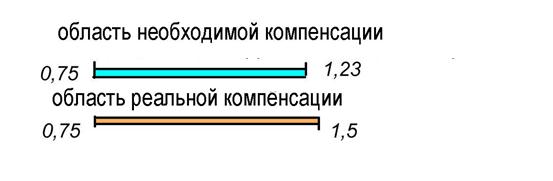
Рисунок 25. Область компенсации

Заключение:

Как видно, наибольшие допуски составляющих звеньев в методе компенсатора (МК). За ним следует теоретико-вероятностный метод (ТВМ). Наиболее жесткие допуски в методе полной взаимозаменяемости (МПВ). Такой метод хорош, но слишком дорогой. Метод компенсатора требует регулировки введения дополнительных деталей и даже узлов но широкие допуски при массовом производстве компенсируют все затраты, в других случаях рационально применение МПВ и ТВМ.

Дата добавления: 2014-01-20