Лекция 3. Классификация экстремальных задач

Классификация экстремальных задач

Экстремальные задачи это задачи, связанные с нахождением наилучших (оптимальных) управляющих воздействий на систему при заданных ограничениях на эти воздействия.

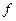В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции при условиях , где и 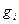- заданные функции, а 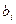- некоторые действительные числа.

Задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функци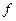и и 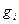линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.

Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач линейного программирования разработан целый ряд эффективных методов, алгоритмов и программ.

Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум или максимум выпуклой (вогнутой) функции, заданной на выпуклом замкнутом множестве.

В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.

Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно - линейного программирования.

В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.

В задачах параметрического программирования целевая функция или функции, определяющие область возможных изменений переменных, либо то и другое зависят от некоторых параметров.

В задачах дробно – линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, также являются линейными.

Выделяют отдельные классы задач стохастического и динамического программирования.

Если в целевой функции или в функциях, определяющих область возможных изменений переменных, содержатся случайные величины, то такая задача относится к задаче стохастического программирования.

Задача, процесс нахождения решения которой является многоэтапным, относится к задаче динамического программирования.

ИТАК, подведем итоги.

Под общей задачей математического программирования будем понимать задачу максимизации скалярной функции

при условиях

и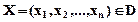

В зависимости от структуры f и g_i задачи математического программирования подразделяются на задачи линейного программирования (f и g_i линейные), параметрического (хотя бы одна из функций f или q_i зависит от некоторого параметра), стохастического (хотя бы одна из функций f или g_i содержит в качестве коэффициентов случайные числа).

Область Д - некоторая область n -мерного эвклидова пространства Rⁿ. Если эта область составляет некоторое подмножество натуральных чисел, то задачи математического программирования рассматриваются как дискретные задачи. Наиболее изученными среди таких задач являются задачи линейного программирования.

В ряде задач линейного и нелинейного прогр-я эк процесс зависит от времени – от нескольких периодов (этапов). При решении таких задач (они называются динамическими) необходимо учитывать поэтапное развитие процесса.Это, например, задача распределения ресурсов между предприятиями по годам планируемого периода. Метод решения задач такого рода составляет сущность динамического программирования.

Дата добавления: 2014-01-11