Моменты инерции сечения

Осевым (экваториальным) моментом инерции сечения называетя геометрическая характеристика, численно равная интегралу: (или осевым моментом инерции плоского сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадраты их расстояний до этой оси). Всегда положительна, может быть равна нулю.

Полярным моментом инерции сечения называется геометрическая характеристика, определяемая интегралом вида: 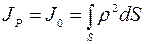, где ρ – расстояние от площадки ds до точки 0 – полюса. Всегда положительна, может быть равна нулю.

Полярный момент инерции можно представить как 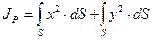, т.е. как сумму осевых моментов инерции.

Центральным моментом инерции сечения называется геометрическая характеристика, определяемая интегралом вида: 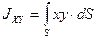. Измеряется в [см⁴], может быть положительной, отрицательной. Если взаимно перпендикулярные оси Х и У, или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю.

Дата добавления: 2014-01-11