Определение напряжений

Крутящие моменты представляют лишь равнодействующие внутренних сил. Фактически в поперечном сечении скручиваемого стержня действуют непрерывно распределенные внутренние касательные напряжения.

При кручении принимаются допущения:

1. Справедлив закон парности касательных напряжений.

2. Справедлива гипотеза Бернулли.

3. Справедлив закон Гука.

4. Радиусы поперечные сечения бруса при деформации не искривляются.

M ₁=10 кН·м ₁ M ₀ =30 кН·м ₂ M ₂=20 кН·м

d

_{1 2}

l =0,5 м l =0,5 м

Эпюра T

10 20 а.

Эпюра σ

б.

Эпюра φ

в.

Рис. 28. Эпюры при кручении

На основании всего этого можем принять, что при кручении в поперечных сечениях возникают только τ, т.е. напряженное состояние во всех точках скручиваемого стержня представляет собой чистый сдвиг (главные напряжения – одно растягивающее, второе сжимающее). Для установления закона распределения касательного напряжения по поперечному сечению скручиваемого стержня рассмотрим более детально деформации стержня (Рис. 29).

Определим угол сдвига элемента АВВ′. Δ АВВ′ - прямоугольный. ВВ′= r · dφ;

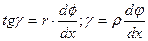(1) – формула для определения угла сдвига, где ρ – радиус кривизны производно выбранного слоя. Закон Гука при сдвиге τ = G·γ. Подставим в закон Гука формулу (1) и получим: (2), т.е при кручении деформации сдвига и касательные напряжения увеличиваются прямо пропорционально расстоянию от центра тяжести к контуру сечения. Исходя из этого,

Μ Y

А В ds

γ_max τds Z

В′ X

r

Μ

dx

Рис. 29. Деформации при кручении

эпюра распределения τ по поперечному сечению будет выглядеть таким образом(Рис.30):

а) в центре тяжести сечния τ = 0;

б) в точка контура сечения τ = τ_max.

τ = τ_max.

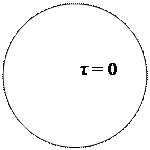
Рис. 30. Эпюра распределения τ по поперечному сечению вала при кручении

Далее: τ ·ds – элементарная внутренняя касательная сила в поперечном сечении (Рис.29), тогда элементарный крутящий момент внутренних сил на площадке ds равен ρ · τ ·ds, а крутящий момент по всей площади поперечного сечения будет представлен как: 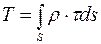(3) – равнодействующий момент касательных напряжений в сечении. Подставим в формулу (3) формулу (2):

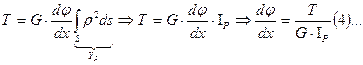подставим формулу(4) в формулу (2):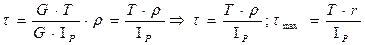, тогда , где W_p – полярный момент сопротивления - величина равная отношению полярных моментов инерции сечения к его радиусу.

Для круга

Для кольца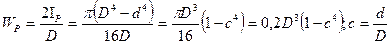

- формула для определения касательных напряжений при кручении, а условие прочности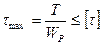

Дата добавления: 2014-01-11