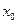Дробный факторный эксперимент

В том случае, когда число влияющих на явление факторов становится значительным (), проведение исследований даже по методу полного факторного эксперимента становится трудоёмким вследствие резкого увеличения числа экспериментов. В этом случае проводится дробный факторный эксперимент, план которого представляет собой часть комбинации полного факторного эксперимента: и т. д. Регрессионная модель может быть получена при числе экспериментов, меньшем чем 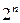; при этом в необходимых случаях могут быть учтены эффекты взаимодействия низших порядков.

Во многих практических случаях взаимодействия высших порядков (тройных, четверных и т. д.) отсутствуют или пренебрежимо малы. Это обусловлено тем, что эксперимент проводится в достаточно узкой области поверхности отклика, которую с определённым приближением можно считать плоскостью (линейное приближение). Кроме того, часто линейная модель достаточна для понимания сущности рассматриваемого физического явления и выполнения практических расчётов.

Для линейного приближения, определяемого уравнением

,

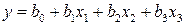требуется найти только четыре коэффициента 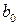, , и 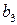. Чтобы решить эту задачу, достаточно провести только четыре вместо восьми экспериментов (). План дробного эксперимента для приведён в таблице 3, в которой столбец 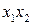(таблицы 2) используется в качестве третьего фактора .

Представленный план является сокращенной (дробной) частью плана полного факторного эксперимента полуреплики.

Таблица 2 – План дробного факторного эксперимента

	+ + + +	– + – +	– – + +	+ – – +

Таблица 3 – План дробного факторного эксперимента для n =3

	+ + + +	– + – +	– – + +	+ – – +

В том случае, когда необходимо учитывать взаимодействия высших порядков, в матрице планирования дробного факторного эксперимента в качестве четвертого фактора (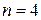) используются столбцы тройного взаимодействия, например – 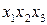(см. таблицу 1).

Полученный таким преобразованием план дробного эксперимента будет представлять собой полуреплику от полного факторного эксперимента при 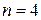, поскольку вместо 16 экспериментов необходимо выполнить только 8, т. е. столько же, сколько и при . Такая полуреплика обозначается 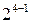(в общем случае ), а её план представлен в таблице 4.

Таблица 4 – План полуреплики для n =4

– + – + – + – +

– – + + – – + +

– – – – + + + +

– + + – + – – +

+ – – + + – – +

+ – + – – + – +

+ + – – – – + +

+ + – – – – + +

+ – + – – + – +

+ – – + + – – +

– + + – + – – +

– – – – + + + +

– – + + – – + +

– + – + – + – +

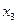
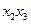
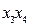
Если число дополнительных факторов равняется двум, то план дробного факторного эксперимента носит название четверти реплики, если трём – одной восьмой реплики и т. д. Общее число экспериментов в этом случае составит , где – число дополнительных факторов.

Составим далее группы одинаковых столбцов, представленных в таблице 4:

.

Отсюда можно сделать вывод о том, что коэффициент , рассчитанный по данным дробного факторного эксперимента 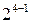, является совместной оценкой, т. е. , где – истинное значение коэффициента регрессии в уравнении регрессионной модели. Аналогично , , .

На основе выполненных восьми экспериментов могут быть рассчитаны семь коэффициентов регрессии, т. е. к четырём линейным членам добавляются три члена, учитывающих парные межфакторные взаимодействия. При этом соответствующие коэффициенты будут являться смешанными оценками двух различных межфакторных взаимодействий.

Полученные таким образом коэффициенты дают достоверные оценки соответствующих эффектов только в тех случаях, когда сопутствующие эффекты пренебрежимо малы. От того, какой столбец взаимодействия высших порядков применяется для оценки линейного эффекта дополнительного фактора, зависят условия смешивания всех оценок. Для анализа условий смешивания при составлении плана дробного факторного эксперимента используется следующий приём.

Выбирается столбец, нужный для оценки линейного эффекта дополнительного фактора (для рассмотренного выше случая – это – равенство, называемое генерирующим соотношением).

После умножения генерирующего соотношения на получим , или с учётом того, что (), будем иметь

.

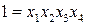Последнее уравнение называется определяющим контрастом; оно позволяет определить с каким из эффектов будет смешан интересующий эффект в составленном плане дробного факторного эксперимента. Умножив обе части равенства определяющего контраста на интересующий фактор, для рассматриваемого случая получим следующие условия смешивания:

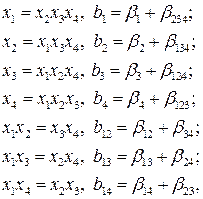
где учтено, что .

При использовании дробного факторного эксперимента важно определить заранее, какие коэффициенты являются несмешанными оценками для соответствующих теоретических коэффициентов. В зависимости от решаемой задачи подбирается дробная реплика, позволяющая получить из эксперимента максимальную информацию. Например, при 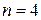выбор в качестве генерирующего соотношения даёт возможность сделать оценку линейного эффекта. 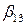Использование генерирующего соотношения имеет смысл в том случае, если более всего интересно знать коэффициенты , и .

При планах большой дробности (1/4 реплики, 1/8 реплика и т. д.) приходится выбирать несколько генерирующих соотношений. Из нескольких вариантов плана затем выбирается наилучший, удовлетворяющий по возможности условию смешивания основных коэффициентов с коэффициентами высшего порядка или с теми коэффициентами, которые не оказывают влияния на явление.

Расчёт коэффициентов регрессии, проверка воспроизводимости экспериментальных данных, статистический анализ математической модели при дробном факторном эксперименте производится так же, как и при полном факторном эксперименте.

Дробный факторный эксперимент имеет определённые недостатки, связанные с исключением из рассмотрения некоторых взаимодействий факторов. Даже в практически известных явлениях экспериментатор затрудняется заранее достоверно утверждать об отсутствии взаимодействия факторов. Поэтому использование дробного факторного эксперимента, особенно большой дробности, требует весьма осторожного и обоснованного подхода.

Дата добавления: 2014-01-20