Нормальный закон распределения случайной величины. Параметры нормального распределения

Математическое описание непрерывных случайных величин (к числу которых относится и ), осуществляется обычно с помощью законов распределения случайной величины. Эти законы определяют связь между возможным значением случайной величины и соответствующей ему плотности вероятности.

Наиболее распространенным при измерениях является нормальный закон распределения (рис. 1.9). Он наблюдается, когда расхождения результатов обусловлены большим числом независимых причин и ни одна из них не доминирует над остальными. На рис. 1.10, а показана кривая нормального распределения для некоторой измеряемой величины Х. По оси абсцисс отложены значения величины Х, а по оси ординат – вероятность их появления р(Х). Кривая нормального распределения симметрична линии, проходящей через центр распределения M[Х] (математическое ожидание), и имеет колоколообразную форму. Рассеяние результатов отдельных измерений относительно центра распределения характеризуется средним квадратическим отклонением s. Математическое ожидание M[Х] является тем значением величины, вокруг которого группируются результаты отдельных измерений. s является мерой рассеяния результатов относительно M[Х], т.е. характеризует форму кривой распределения.

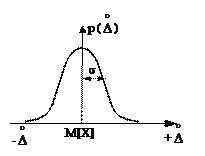
а	б

Рис. 1.10. Кривые нормального распределения: а – случайной величины Х, б – случайной погрешности

Перенеся начало координат в точку M[Х], получим кривую распределения случайной погрешности (рис. 1.10, б).

На рис. 1.11 приведены кривые нормального распределения при различных значениях s (рассеяния результатов). Сравнивая их между собой, можно установить, что рассеяние для кривой 2 меньше, чем для кривой 3, но больше, чем для кривой 1. Очевидно, что наиболее высокая сходимость наблюдается для результатов измерений, распределенных в соответствии с кривой 1.

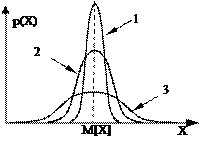
Рис. 1.11. Кривые нормального распределения с разным рассеянием значения величины, s₁ < s₂ < s₃

Математическое выражение для описания кривой нормального распределения случайной величины (рис. 1.10, а), предложенное Гауссом, имеет вид

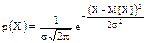(1.10)

Для описания кривой нормального распределения случайной погрешности (рис. 1.10, б) это выражение можно переписать в виде

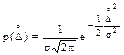(1.11)

M[Х] и s являются двумя важнейшими параметрами нормального распределения случайной величины. Достаточно знать эти параметры, чтобы задать нормальное распределение.

Дата добавления: 2014-01-11