Признаки количественные

Признаки качественные

Качественные признаки (атрибутивные) – это признак отдельное значение которого выражаются в виде понятий, наименований. Это признаки, которыми объект обладает либо не обладает. Они не поддаются непосредственному измерению (например, цвет волос, специализация, квалификация, национальность, территориальная принадлежность, образование и т.п.).

Если атрибутивные признаки принимают только одну из двух противоположных значений, их называют Альтернативными. Например пол (мужской, женский)

Количественный признак – это признак определяющее значение которого имеют количественные выражения например (рост – 155 см.) т.о. это результаты подсчета или измерения

Каждый объект изучения может обладать целым рядом статистических признаков, но от объекта к объекту одни признаки меняются, остаются неизменными.

Меняющиеся признаки от одного объекта к другому принято называть варьирующимися. Именно эти признаки изучаются статистикой.)например размеры обуви

Вариация- это многообразие изменения величины признака у отдельных единиц в совокупности наблюдения (вариации з.п. 5000, 10000, 15000 тыс.)

Отдельные значения признака называют вариантами признака.

Переменная (английский термин variable) — это то, что можно измерять, контролировать или чем можно манипулировать в исследованиях. Иными словами, переменная — это то, что варьируется, изменяется, а не является постоянным (от английского корня var).

Переменная — это величина, характеризующаяся множеством значений, которое она может принимать.[1] При этом может иметься ввиду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.

В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.

Например, измеряя давление или содержание лейкоцитов в крови, вы получаете различные значения у разных пациентов или значения для одного и того же пациента в разное время суток. Измеряя уровень осадков, получаете различные значения в разные дни недели, а также различные значения в одни и те же дни в разных точках географической карты.

Другие примеры переменных из разных областей: анкетные данные, систолическое давление пациентов, количество лейкоцитов в крови, цена акций, товаров, услуг, потребление, инвестиции, доход, государственные закупки товаров и услуг, инструмент государственного регулирования (в экономике); рейтинг программ, доля зрителей, количество посещений сайта (в рекламе); скорость, температура, объем, масса в (физике) и т. д.

Очевидно, что это очень разные по своим свойствам переменные, и поэтому можно сказать, что переменные отличаются характеристиками, в частности, той ролью, которую они играют в исследованиях, типом измерений и т. д.

Переменные и постоянные величины - величины, которые в изучаемом вопросе принимают различные значения либо, соответственно, сохраняют одно и то же значение. Например, при изучении падения тела расстояние последнего от земли и скорость падения — переменные величины, ускорение же (если пренебречь сопротивлением воздуха) — величина постоянная. Элементарная математика рассматривала все изучаемые ею величины как постоянные. Понятие переменной величины возникло в математике в 17 в. под влиянием запросов естествознания, выдвинувшего на первый план изучение движения — процессов, а не только состояний. Это понятие не укладывалось в формы, выработанные математикой древности и средних веков, и требовало для своего выражения новых форм. Такими новыми формами явились буквенная алгебра и аналитическая геометрия Р. Декарта.

Рене Декарт (1596- 1650)

впервые показал, как можно применить математику для наглядного изображения и математического анализа самых разнообразных явлений природы и общества. Он предложил изображать связи между явлениями природы кривыми линиями, а последние записывать алгебраическими уравнениями. Положив в основу своей философии понятие о движущейся материи, Декарт внес движение и в математику.

Если до Декарта математика имела метафизический характер, оперируя с постоянными величинами, то с трудами Декарта в математику, а вместе с тем и во все естествознание вошла диалектика. В работах Декарта по математике впервые появляются переменные величины и указывается, как можно строгие законы геометрии перевести на алгебраический язык и использовать при решении различных задач, на первый взгляд далеких от математики.

Декарт формулирует "правила метода", с помощью которого можно прийти к истине. Первоначально мыслившиеся Декартом весьма многочисленными, в "Рассуждении о методе", они сводятся им к четырем основным положениям, составляющим "квинтэссенцию" европейского рационализма:

1) начинать с несомненного и самоочевидного, т. е. с того, противоположное чему нельзя помыслить,

2) разделять любую проблему на столько частей, сколько необходимо для ее эффективного решения,

3) начинать с простого и постепенно продвигаться к сложному,

4) постоянно перепроверять правильность умозаключений.

Существует несколько легенд об изобретении системы координат, которая носит имя Декарта.

Однажды Рене Декарт весь день пролежал в кровати, думая о чем-то, а муха жужжала вокруг и не давала ему сосредоточиться. Он стал размышлять, как бы описать положение мухи в любой момент времени математически, чтобы иметь возможность прихлопнуть ее без промаха. И... придумал декартовы координаты, одно из величайших изобретений в истории человечества.

Проследим путь открытия системы координат согласно этой легенде в картинках.

Время открытия: 1637 год.

На рисунке условно показаны три стены кабинета:

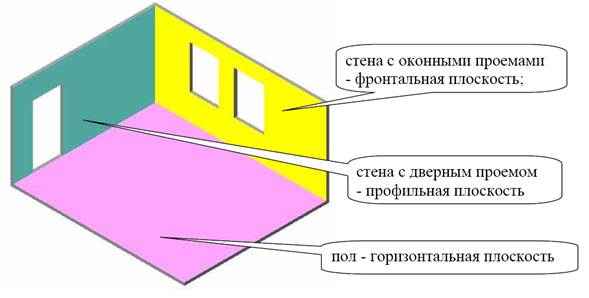
Обратите внимание! Каждые две плоскости пересекаются по прямой линии.

1. На фронтальную

плоскость садится муха

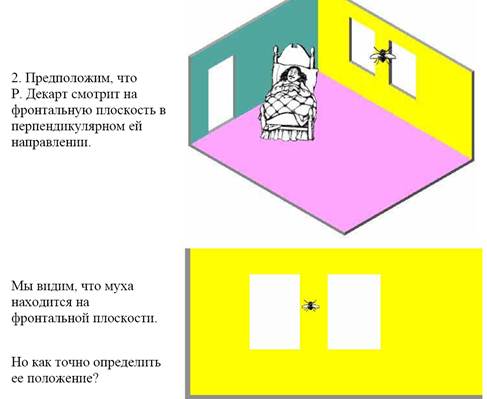
3. Эврика!

Нужно взять две взаимно перпендикулярные числовые прямые.

Точку пересечения прямых обозначим как О - начало системы координат.

Одну из прямых назовем ось X, другую - ось Y.

На нашем рисунке расстояние между делениями на числовых прямых равно единице.

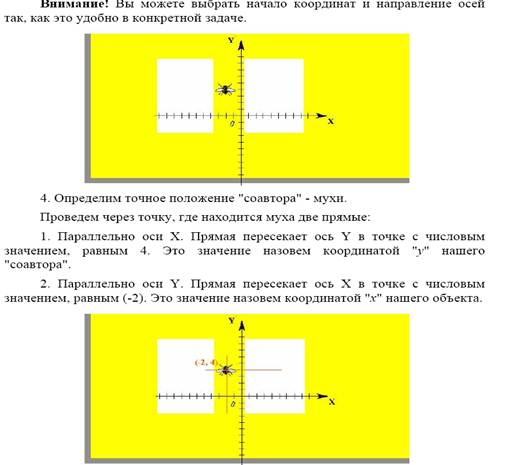
Принято координаты объекта, обычно точки, записывать в форме (x, y).

Для нашей мухи мы можем сказать, что она находится в точке с координатами (-2, 4).

Задача точного определения положения мухи решена!

Новизна идеи состоит в том, что положение точки или объекта на плоскости определяетcя с помощью двух пересекающихся осей.

Таким образом, Декарт является первооткрывателем аналитической геометрии, в основе которой лежит изобретенный им метод координат. Этот метод, как известно, применялся и ранее Декарта. Значительное развитие он получил у Ферма. Тем не менее у Декарта он приобрел гораздо большее значение, так как при помощи этого метода Декарту удалось указать новые направления в дальнейшем развитии математики.

В 1637 году вышел в свет главный математический труд Декарта, «Рассуждение о методе» (полное название: «Рассуждение о методе, позволяющем направлять свой разум и отыскивать истину в науках»).

В этой книге излагалась аналитическая геометрия, а в приложениях — многочисленные результаты в алгебре, геометрии, оптике (в том числе — правильная формулировка закона преломления света) и многое другое.

Особо следует отметить переработанную им математическую символику Виета, с этого момента близкую к современной. Коэффициенты он обозначал a, b, c…, а неизвестные — x, y, z. Натуральный показатель степени принял современный вид (дробные и отрицательные утвердились благодаря Ньютону). Появилась черта над подкоренным выражением. Уравнения приводятся к канонической форме (в правой части — нуль).

Символическую алгебру Декарт называл «Всеобщей математикой», и писал, что она должна объяснить «всё относящееся к порядку и мере».

Математическому гению мыслителя мы обязаны введением в употребление привычных теперь обозначений с помощью латинских букв постоянных и переменных величии, а также обозначением степеней. Декарт значительно улучшил систему обозначений, введя общепринятые знаки для переменных величин (х, у, z,...) и коэффициентов (а, b, с,...), а также обозначения степеней (х⁴, a⁵,...).

Благодаря Декарту алгебра как в своих основных методах, так и в символике приняла тот характер, который ей присущ и в настоящее время. Декарт придавал особое значение математике. Он исходил из того убеждения, что математика должна быть образцом для всякой другой науки. По его мнению, только та наука может считаться истинной, которая в своем построении следует математике, так как все выводы математики являются логически необходимыми, дающими полную достоверность.

В "Геометрии" (1637г.) Декарта впервые ввел понятие переменной величины и функции. Переменная величина выступала у Декарта как отрезок переменной длины и постоянного направления (текущая координата точки, описывающей своими движениями кривую) и как непрерывная числовая переменная, пробегающая совокупность чисел, составляющих координатный отрезок. Двоякий образ переменной обусловил взаимопроникновение геометрии и алгебры, к которому стремился Декарта. Алгебра Декарта в отличие от алгебры Ф. Виета, имеет всегда один основной элемент - линейный отрезок, операции над которым приводят опять-таки к некоторому отрезку. Эти отрезки по свойствам равносильны действительным числам. У Декарта действительное число выступало как отношение длины отрезка к единичному, хотя сформулировал такое определение числа лишь И. Ньютон. Отрицательные числа получили у Декарта реальное истолкование в виде направленных координат.

Впервые уравнение кривой исследовал Р. Декарт в 1638 году, однако он построил только петлю в первом координатном угле, где x и y принимают положительные значения. Декарт полагал, что петля симметрично повторяется во всех четырёх координатных четвертях, в виде четырёх лепестков цветка. В то время эта кривая называлась цветком жасмина (англ. jasmine flower, фр. fleur de jasmin).

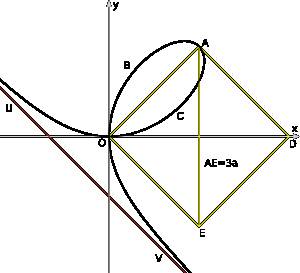
Математические исследования Декарта тесно связаны с его работами по философии и физике. В "Геометрии" (1637г.) Декарта впервые ввел понятие переменной величины и функции. Переменная величина выступала у Декарта как отрезок переменной длины и постоянного направления (текущая координата точки, описывающей своими движениями кривую) и как непрерывная числовая переменная, пробегающая совокупность чисел, составляющих координатный отрезок. Двоякий образ переменной обусловил взаимопроникновение геометрии и алгебры, к которому стремился Декарта.

Средь неизбежного круговорота сил

И вечности, поставленной на карту,

Должна признаться всё же, как мне мил

“Цветок жасмина” * – парадокс Декарта. **

Я по его спирали медленно брожу,

Теряясь в точках обреченно,

Брожу – и постоянство нахожу,

Касаясь листьев облегченно.

Круговорот петли заманит нас в пути

Своей дугой, растущей неуклонно,

Всю мимолётность мига обрести

В мечтах, глядящих благосклонно

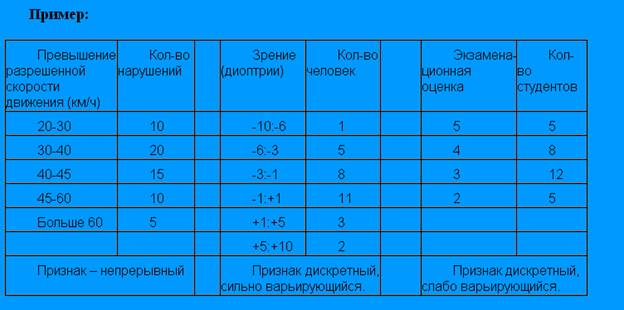
Если две варианты признака в данной совокупности могут отличаться одна от другой не менее чем на определенное число или вообще совпадают, т.е. они могут принимать лишь отдельные значения из некоторого ряда чисел, то такие данные называют дискретными (число учеников в классах школы; количество баллов, которые набирает ученик при тестировании, количество прожитых лет, число попаданий и промахов при серии выстрелов. и т. п.).

Если же две варианты признака могут отличаться одна от другой на произвольно малую величину, т.е. могут принимать любые значения в определенном интервале, то такие данные называют непрерывными (процент учеников, которые имеют достаточный уровень подготовки по предмету в разных классах; время, за которое ученики пробежали 60 м на соревнованиях; продолжительность работы электронных ламп; время работы механизма, скорость движения,температура воздуха и т. п.).

Ряд значений признака, или вариант, полученных вследствие массового обследования однородных вещей или явлений, размещенных в порядке возрастания или убывания их величин, вместе с соответствующими частотами (или относительными частотами) называют вариационным рядом.

Если в вариационном ряде значения признака (варианты) заданы в виде отдельных конкретных чисел, то такой ряд называют дискретным.

Если в вариационном ряде значения признака заданы в виде интервалов, то такой ряд называют интервальным. Если в интервальном вариационном ряде в двух последовательных интервалах верхнее предельное значение признака одного интервала равняется нижнему предельному значению второго, условно будем считать, что это число принадлежит второму интервалу. Разность между верхней и нижней границами интервала называют шириной этого интервала.

Интервальный ряд

Дата добавления: 2014-01-20