Линейные системы

Рассмотрим систему двух линейных уравнений:

. (4.4)

Здесь a, b, c, d - константы, x, y ‑ декартовы координаты на фазовой плоскости.

Общее решение будем искать в виде:

. (4.5)

Подставим эти выражения в (4.4) и сократим на e^lt:

(4.6)

Алгебраическая система уравнений (4.6) с неизвестными A, B имеет ненулевое решение лишь в том случае, если ее определитель, составленный из коэффициентов при неизвестных, равен нулю:

.

Раскрывая этот определитель, получим характеристическое уравнение системы:

. (4.7)

Решение этого уравнения дает значения показателя l _1,2, при которых возможны ненулевые для A и B решения уравнения (4.6). Эти значения суть

. (4.8)

Если подкоренное выражение отрицательно, то l _1,2 комплексно сопряженные числа. Предположим, что оба корня уравнения (4.7) имеют отличные от нуля действительные части и что нет кратных корней. Тогда общее решение системы (4.4) можно представить в виде линейной комбинации экспонент с показателями l ₁, l ₂:

_(4.9)

Для анализа характера возможных траекторий системы на фазовой плоскости используем линейное однородное преобразование координат, которое позволит привести систему к каноническому виду:

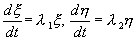, (4.10)

допускающее более удобное представление на фазовой плоскости по сравнению с исходной системой (4.4). Введем новые координаты ξ, η по формулам:

(4.1)

Из курса линейной алгебры известно, что в случае неравенства нулю действительных частей l ₁, l ₂ исходную систему (4.4) при помощи преобразований (4.11) всегда можно преобразовать к каноническому виду (4.10) и изучать ее поведение на фазовой плоскости ξ, η. Рассмотрим различные случаи, которые могут здесь представиться.

Корни λ₁, λ₂ – действительны и одного знака

В этом случае коэффициенты преобразования действительны, мы переходим от действительной плоскости x,y к действительной плоскости ξ, η. Разделив второе из уравнений (4.10) на первое, получим:

. (4.12)

Интегрируя это уравнение, находим:

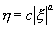, где . (4.13)

Условимся понимать под λ₂ корень характеристического уравнения с большим модулем, что не нарушает общности нашего рассуждения. Тогда, поскольку в рассматриваемом случае корни λ₁, λ₂ – действительны и одного знака, a >1, и мы имеем дело с интегральными кривыми параболического типа.

Все интегральные кривые (кроме оси η, которой соответствует ) касаются в начале координат оси ξ, которая также является интегральной кривой уравнения (4.11). Начало координат является особой точкой.

Выясним теперь направление движений изображающей точки вдоль фазовых траекторий. Если λ₁, λ₂ – отрицательны, то, как видно из уравнений (4.10), |ξ|, |η| убывают с течением времени. Изображающая точка приближается к началу координат, никогда, однако, не достигая его. В противном случае это противоречило бы теореме Коши, которая утверждает, что через каждую точку фазовой плоскости проходит лишь одна фазовая траектория.

Такая особая точка, через которую проходят интегральные кривые, подобно тому, как семейство парабол проходит через начало координат, носит название узла(рис. 4.5)

Рис. 4.5. Особая точка типа узел на плоскости канонических координат ξ, η

Состояние равновесия типа узел при λ₁, λ₂ < 0 устойчиво по Ляпунову, так как изображающая точка по всем интегральным кривым движется по направлению к началу координат. Это устойчивый узел. Если же λ₁, λ₂ > 0, то |ξ|, |η| возрастают с течением времени и изображающая точка удаляется от начала координат. В этом случае особая точка – неустойчивый узел.

На фазовой плоскости x, y общий качественный характер поведения интегральных кривых сохранится, но касательные к интегральным кривым не будут совпадать с осями координат. Угол наклона этих касательных будет определяться соотношением коэффициентов α, β, γ, δ в уравнениях (4.11).

Корни λ₁, λ₂ – действительны и разных знаков.

Преобразование от координат x,y к координатам ξ, η опять действительное. Уравнения для канонических переменных снова имеют вид (4.10), но теперь знаки λ₁, λ₂ различны. Уравнение фазовых траекторий имеет вид:

где , (4.14)

Интегрируя (4.14), находим

(4.15)

Это уравнение определяет семейство кривых гиперболического типа, где обе оси координат – асимптоты (при a =1 мы имели бы семейство равнобочных гипербол). Оси координат и в этом случае являются интегральными кривыми – это будут единственные интегральные кривые, проходящие через начало координат. Каждая из них состоит из трех фазовых траекторий: из двух движений к состоянию равновесия (или от состояния равновесия) и из состояния равновесия. Все остальные интегральные кривые – суть гиперболы, не проходящие через начало координат (рис. 4.6) Такая особая точка носит название «седло». Линии уровня вблизи горной седловины ведут себя подобно фазовым траекториям в окрестности седла.

Рис. 4.6. Особая точка типа седло на плоскости канонических координат ξ, η

Рассмотрим характер движения изображающей точки по фазовым траекториям вблизи состояния равновесия. Пусть, например, λ₁>0, λ₂<0. Тогда изображающая точка, помещенная на оси ξ, будет удаляться от начала координат, а помещенная на оси η – будет неограниченно приближаться к началу координат, не достигая его за конечное время. Где бы ни находилась изображающая точка в начальный момент (за исключением особой точки и точек на асимптоте η =0), она в конечном счете будет удаляться от состояния равновесия, даже если в начале она движется по одной из интегральных кривых по направлению к особой точке.

Очевидно, что особая точка типа седла всегда неустойчива. Только при специально выбранных начальных условиях на асимптоте η =0 система будет приближаться к состоянию равновесия. Однако это не противоречит утверждению о неустойчивости системы. Если считать, что все начальные состояния системы на фазовой плоскости равновероятны, то вероятность такого начального состояния, которое соответствует движению по направлению к особой точке, равна нулю. Поэтому всякое реальное движение будет удалять систему от состояния равновесия. Переходя обратно к координатам x,y, мы получим ту же качественную картину характера движения траекторий вокруг начала координат.

Пограничным между рассмотренными случаями узла и седла является случай, когда один из характеристических показателей, например λ ₁, обращается в нуль, что имеет место, когда определитель системы – выражение ad-bc=0 (см. формулу 4.8 ). В этом случае коэффициенты правых частей уравнений (4.4) пропорциональны друг другу:

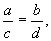
и система имеет своими состояниями равновесия все точки прямой:

Остальные интегральные кривые представляют собой семейство параллельных прямых с угловым коэффициентом , по которым изображающие точки либо приближаются к состоянию равновесия, либо удаляются от него в зависимости от знака второго корня характеристического уравнения λ₂ = a+d. (Рис.4.7) В этом случае координаты состояния равновесия зависят от начального значения переменных.

Рис. 4.7. Фазовый портрет системы, один из характеристических корней которой равен нулю, а второй отрицателен.

Корни λ₁, λ₂ – комплексные сопряженные

В этом случае при действительных x и y мы будем иметь комплексные сопряженные ξ, η (4.10). Однако, вводя еще одно промежуточное преобразование, можно и в этом случае свести рассмотрение к действительному линейному однородному преобразованию. Положим:

(4.16)

где a,b, и u,v – действительные величины. Можно показать, что преобразование от x,y к u,v является при наших предположениях действительным, линейным, однородным с детерминантом, отличным от нуля. В силу уравнений (4.10, 4.16) имеем:

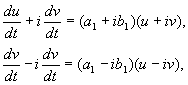
откуда

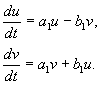(4.17)

Разделив второе из уравнений на первое, получим:

которое легче интегрируется, если перейти к полярной системе координат (r, φ). После подстановки получим 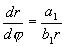, откуда:

. (4.18)

Таким образом, на фазовой плоскости u, v мы имеем дело с семейством логарифмических спиралей, каждая из которых имеет асимптотическую точку в начале координат. Особая точка, которая является асимптотической точкой всех интегральных кривых, имеющих вид спиралей, вложенных друг в друга, называется фокусом ( рис.4.8 ).

Рис. 4.8. Фазовый портрет системы в окрестности особой точки типа фокус на плоскости координат u, v.

Рассмотрим характер движения изображающей точки по фазовым траекториям. Умножая первое из уравнений (4.17) на u, а второе на v и складывая, получаем:

где

Пусть a ₁ < 0 (a ₁ =Reλ). Изображающая точка тогда непрерывно приближается к началу координат, не достигая его в конечное время. Это означает, что фазовые траектории представляют собой скручивающиеся спирали и соответствуют затухающим колебаниям переменных. Это – устойчивый фокус.

В случае устойчивого фокуса, как и в случае устойчивого узла, выполнено не только условие Ляпунова, но и более жесткое требование. Именно, при любых начальных отклонениях система по прошествии времени вернется как угодно близко к положению равновесия. Такая устойчивость, при которой начальные отклонения не только не нарастают, но затухают, стремясь к нулю, называют абсолютной устойчивостью.

Если в формуле (4.18) a ₁>0, то изображающая точка удаляется от начала координат, и мы имеем дело с неустойчивым фокусом. При переходе от плоскости u,v к фазовой плоскости x,y спирали также останутся спиралями, однако будут деформированы.

Рассмотрим теперь случай, когда a ₁=0. Фазовыми траекториями на плоскости u, v будут окружности которым на плоскости x,y соответствуют эллипсы:

Таким образом, при a₁ =0 через особую точку x= 0, y= 0 не проходит ни одна интегральная кривая. Такая изолированная особая точка, вблизи которой интегральные кривые представляют собой замкнутые кривые, в частности, эллипсы, вложенные друг в друга и охватывающие особую точку, называется центром.

Таким образом, возможны шесть типов состояния равновесия в зависимости от характера корней характеристического уравнения (4.7). Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 4.9.

Рис. 4.9. Типы фазовых портретов в окрестности стационарного состояния для системы линейных уравнений (4.4).

Пять типов состояния равновесия грубые, их характер не изменяется при достаточно малых изменениях правых частей уравнений (4.4). При этом малыми должны быть изменения не только правых частей, но и их производных первого порядка. Шестое состояние равновесия – центр – негрубое. При малых изменениях параметров правой части уравнений он переходит в устойчивый или неустойчивый фокус.

Дата добавления: 2014-01-20