Пример формулировки и решения задачи линейного программирования

Задачи линейного программирования достаточно содержательны с практической точки зрения и при этом, как правило, имеют решение в классе точных методов, представителем которых является, например, симплекс-метод.

Рассмотрим практический пример из строительства.

Имеется растворный узел, производящий бетон двух видов (в зависимости от расхода цемента, песка и щебня). Исходные данные по работе такого узла могут быть представлены таблицей 3.6.1.

Таблица 3.6.1. Исходные данные по работе бетонного узла.

	Расход сырья на единицу
Вид сырья	продукции	Запас сырья
	1^й тип бетона	2^й тип бетона
Цемент	0.25	0.25	1.5
Песок	0.25	0.5	2.5
Щебень	0.5	0.25	2.5
Цена ед. продукции

Пусть 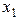– количество выпущенного бетона первого типа, – количество выпущенного бетона второго типа. Тогда доход бетонного узла определяется формулой

.

При этом имеет место следующий расход материалов, ограничиваемый их заданными запасами:

– цемент: ;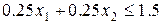

– песок: ;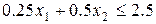

– щебень: .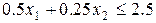

В правой части данных неравенств присутствует ограничение, связанное с реальным запасом материалов в растворном узле.

Задача состоит в таком планировании производства (то есть определени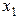и и 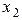– плана выпуска), при котором величина дохода 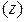максимальна, т.е. нужно найти точку максимума функции z

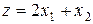
при ограничениях

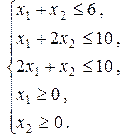
Обратим внимание на то, что приведенные неравенства для их упрощения умножены на число «4». Последние два неравенства являются очевидным ограничением на параметры x ₁, x ₂, поскольку в нашем случае объем выпускаемой продукции не может оказаться отрицательным.

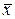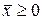Соответствующая матричная формулировка задачи следующая: найти вектор , при котором функция достигает максимума, при ограничениях и , где

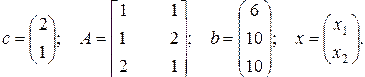
Геометрическая интерпретация решения задачи. Как следует из аналитической геометрии, каждое из представленных выше неравенств-ограничений задает некоторую полуплоскость. Их совокупность определяет некоторый выпуклый многоугольник 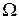, изображенный на рис. 3.6.1. Его называют многоугольник ограничений. Очевидно, что искомые значения 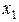и принадлежат этому многоугольнику.

Среди точек области 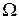необходимо отыскать такую, в которой функция принимала бы максимальное значение.

Выясним геометрический смысл целевой функции . Ее графиком является плоскость, имеющая пересечение с координатной плоскостью x ₁ 0 x ₂ по линии 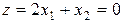(см. рис. 3.6.1).

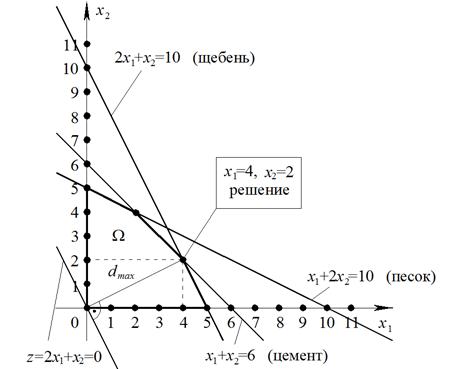
Рис. 3.6.1. Геометрическая интерпретация. Многоугольник ограничений.

Из аналитической геометрии известно, что расстояние 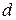от точки 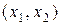до прямой 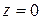, где 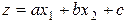, определяется по общей формуле

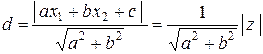. (3.6.13)

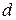Поскольку в рассматриваемой задаче , то пропорциональна и максимум значения достигается в точке, максимально удаленной от прямой .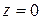

Теперь задачу можно поставить: среди точек многоугольника 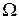требуется найти точку, наиболее удаленную от прямой .

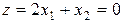Из рис. 3.6.1 видно, что такой точкой будет точка пересечения прямых:

и ,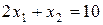

т.е. одна из вершин многоугольника. Решая эту систему уравнений, находим координаты искомой точки:

; .

Следовательно, в соответствии оптимальному плану (наибольший доход) нужно из имеющегося сырья выпускать 4 единицы бетона первого типа и 2 единицы бетона второго типа. При этом будет получен доход

.

Предложенный метод решения – геометрический. Он хорош лишь для случая двух-трех переменных.

Дата добавления: 2014-01-20