Решение вариационной задачи

Разобьем отрезок 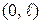на 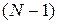часть (на конечные элементы), как показано на рис. 3.7.2. Введем обозначения:

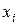– координата начала (левого края) 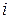-го конечного элемента (точка разбиения);

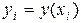– значение искомой функции в 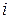-ой точке разбиения;

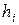– длина 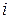-го конечного элемента

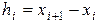. (3.7.9)

Представим интеграл 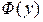в виде суммы интегралов

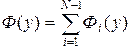, (3.7.10)

где 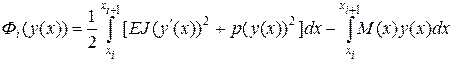. (3.7.11)

Искомая функция 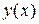принимает на краях элемента соответственно значения 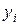и 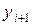. Примем, что внутри каждого 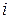-го элемента (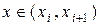) она линейная (рис. 3.7.3):

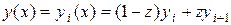, (3.7.12)

где 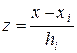, 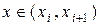. (3.7.13)

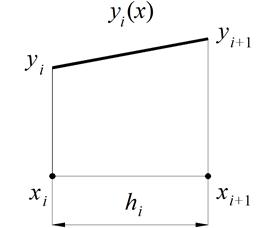
Рис. 3.7.3. Линейная аппроксимация неизвестных.

Введем обозначения:

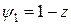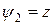; ; (3.7.14)

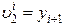; . (3.7.15)

Следовательно,

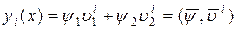, (3.7.16)

где 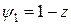; 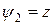(3.7.17)

– так называемые функции формы (рис. 3.7.4).

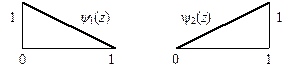
Рис. 3.7.4. Функции формы конечного элемента.

Производные функций формы по z, очевидно, имеют вид:

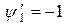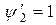; . (3.7.18)

Величины

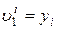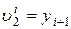; (3.7.19)

называются локальными неизвестными i-го элемента.

Векторы функций форм и локальных неизвестных соответственно определяются следующим образом:

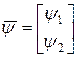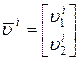; . (3.7.20)

Подставляя 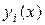(3.7.16) в 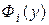(3.7.11) и делая замену переменных x на z, получим:

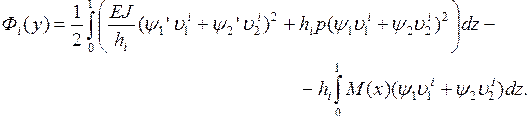(3.7.21)

Вычисляя интегралы и приводя подобные члены, получим:

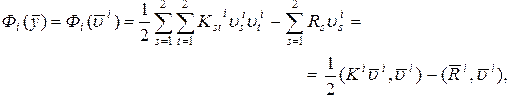(3.7.22)

где матрица 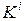называется матрицей жесткости i-го конечного элемента.

В свою очередь ее элементы вычисляются по формуле

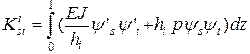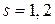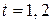, , . (3.7.23)

Вектор 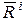называется вектором нагрузки i-го элемента. Его компоненты вычисляются по формуле

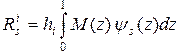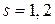, . (3.7.24)

Опуская промежуточные выкладки, можем записать:

; (3.7.25)

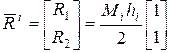, где 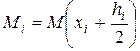. (3.7.26)

Глобальные матрица жесткости и вектор нагрузки. Общий функционал представляющий сумму функционалов по элементам примет вид:

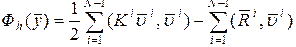, (3.7.27)

где 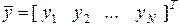. (3.7.28)

Из определения вектора 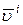следует, что

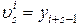. (3.7.29)

Заменяя в (3.7.27) компоненты векторов 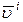на компоненты вектора 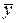и опуская промежуточные выкладки, получим:

, (3.7.30)

где матрица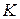называется глобальной матрицей жесткости, ее элементы вычисляются по формулам:

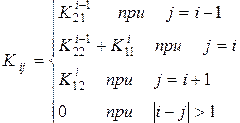(3.7.31)

Общая структура глобальной матрицы жесткости следующая:

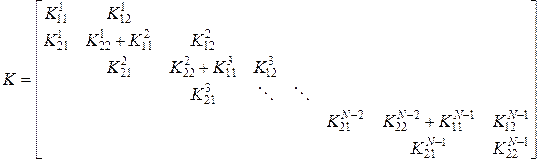. (3.7.32)

Вектор 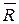называется глобальным вектором нагрузки. Его компоненты вычисляются по формулам:

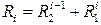. (3.7.33)

Общая структура глобального вектора нагрузки имеет вид:

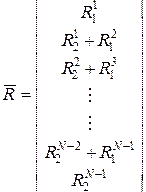. (3.7.34)

При программировании вычисления элементов глобальной матрицы жесткости и правой части наиболее удобными являются формулы (формулы «конечных вкладов»):

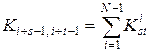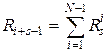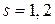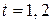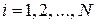, , , , . (3.7.35)

На практике, как правило, локальные матрицы жесткости и векторы нагрузки (3.7.25), (3.7.26) для конкретного вида элементов конструкций известны заранее (существуют специальные библиотеки конечных элементов). Они соответствуют математическому выражению под знаком интеграла в исходном функционале и конфигурации конечных элементов. Поэтому основная задача расчетчика состоит в разбиении конструкции на конечные элементы и формировании глобальной матрицы жесткости и глобального вектора нагрузки (хотя и здесь имеются стандартные алгоритмы).

Учет закреплений. Для того, чтобы удовлетворить условию 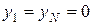, следует приравнять нулю элементы первых и последних строк и столбцов матрицы 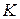, а затем положить 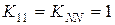и .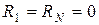

Решение задачи получаем из решения глобальной системы уравнений

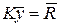. (3.7.36)

Дата добавления: 2014-01-20