Производная по направлению. Пусть диффенцируемая функция двух переменных

Пусть диффенцируемая функция двух переменных. Рассмотренные ранее частные производные от функции двух переменных являются «производными в направлении координатных осей». Например, при нахождении приращение получает переменная x, изменяясь от x до вдоль оси Ox. Целесообразно поставить вопрос об определении и вычислении производной по любому направлению.

Пусть направление движения точки 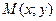плоскости будет показывать вектор где 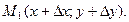Обозначим длину вектора 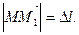При этом функция получит приращение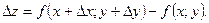

Производной функции в точке 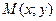в направлении вектора называется предел отношения 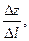при 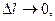если он существует. Обозначается 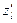или То есть

Производная по направлению характеризует скорость изменения функции в направлении вектора. Если 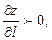то функция возрастает в направлении вектора , если 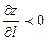, то функцияубывает в направлении вектора .

Механический (физический) смысл производной по направлению состоит в том, что она характеризует мгновенную скорость изменения функции в точке внаправлении вектора .

Для вычисления производной по направлению функции двух переменных используют формулу:

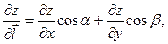
где и 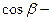направляющие косинусы, т.е. косинусы углов, образуемых вектором с осями координат.

Пример.. Найти производную функции в точке в направлении, идущем от этой точки к точке

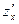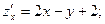
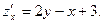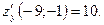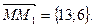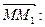
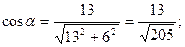
Решение. Вычислим и Найдем значения этих производных в точке : Найдем координаты вектора Вычислим направляющие косинусы вектораДля вычисления производной функции 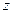по направлению подставим полученные выражения в формулу: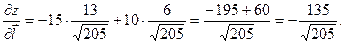

Дата добавления: 2014-01-20